I’ve found surprsingly few explanations in the wild that satisfy me. Plenty that tell you how to make them, some that explain it for data scientists, but nothing that really reflects much on what they might ‘mean’ for arbitary sounds, from a musical perspective. I think a complete physical interpretation probably isn’t possible, but here’s a couple of possible ways of thinking about them.
Way 1: Dimension Reduction for Audio Spectra
Possibly makes most sense for a black box approach, we can just think of the process like we do another dimensionality reduction techniques that do something magical, but at the cost of directly interprable outputs. However in this case, especially tailored for applying to audio spectra, and warped in such a way as to coincide with human auditory perception, in principle.
This isn’t too outlandish: one of the steps in obtaining MFCCs – the step that gets you from the spectral domain into the ceptral domain – can be thought of as an approximation to Principal Components Analysis (for which y’all will soon have an object), which is often the first go-to simple dimensionality reduction technique people reach for.
The auditory tailoring comes from the mel bit: spectral bins are lumped together into mel-bands to mitigate the linear-frequency-ness of DFTs vs the very-nonlinear-frequency-ness of how we hear; and also (more loosely) from the fact that we also take a log of the spectrum, which has a compressive effect on the amplitudes.
Way 2: As a Signal Processing Thing
This is more slippery, because it involves trying to work out what ‘ceptral’ actually means in physical terms, and that’s hard, but perhaps revealing.
The step in the process I glossed over above as being ‘like PCA’ is (normally, for MFCCs) a discrete cosine transform. For our purposes, let’s just regard it for now as a further kind of frequency analysis (like the DFT we’ve already done), but applied to the spectrum, not the time domain signal.
What does that get us? Well, the first frequency analysis tells us something about periodicities in the time domain signal. So, by extension, the second frequency analysis is telling us something about periodicities in the spectrum. For instance, if you have a spectrum with a very clear partial structure (viz. periodic peaks), then you would expect a frequency analysis of that to display a clear singular peak, at some point relating to the spacing of the harmonics.
However, just performing a frequency analysis of a spectrum isn’t all that’s needed to get you a cepstrum: a preceding logarithm is essential as well. Leaving aside that the log happens to have desireable compression effects, as above, it also has a very important property: log(ab) = log(a) + log(b). I.e. scaling relationships become mixing relationships after a log. Even better, when we recall that convolutions in time become multiplications in frequency, it follows that temporal convolutions have been reduced to something as simple and seperable as additions in the cepstrum.
This explains part of the original motivation for using cepstra in speech research, where you have a straightforwardly convolutional model of the glottal pulse being filtered (convolved with the time-varying response of) the vocal tract. Cepstral techniques allow some attempt to be made at separating one from the other: i.e. an applied spectral envelope to an underlying source. MFCCs, as a more compressed version of the same idea, turned out to have better matching performance for speech than most other things. It’s not clear (to me) how rigoursly their application to non-speech sound has been probed, but they certainly do ‘well enough’ much of the time.
If you’re still reading, and were wondering about this discrete cosine transform business, and why we use that: the original formulations of ceptral processing do use DFTs. However, for the purposes of data sciency stuff, the DCT does some desireable things. First, it is real-valued, making its outputs easier to deal with than the complex-valued DFT. Second is the property mentioned above, in that it approximates Principal Component Analysis: what this means is that the individual components of the DCT – whilst harder to interpret physically – have a desireable statistical qualities of being largely uncorrelated with each other, meaning that the individual coefficients of MFCCs can safely be treated as statisically independent from one another (greatly simplifying their use in, e.g., machine learning models), but also (I think???) that later coefficients account for less of the overal variance of the source spectrum.
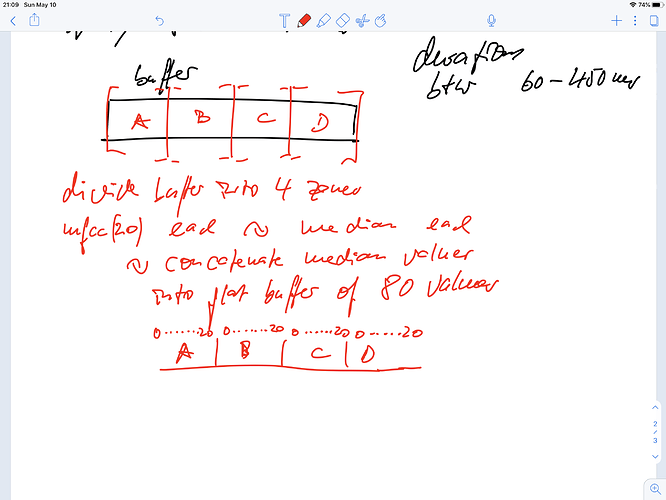
** How to make MFCCs **
DFT → squared magnitudes (I think) → mel band filtering → log → dct → throw some away
The 0th coefficient we regard as a sort of energy measure because it represents the equivalent of DC in the spectral shape: i.e that thing with no period (or, rather, a single period covering the whole spectrum) that accounts for its overall, gross height.