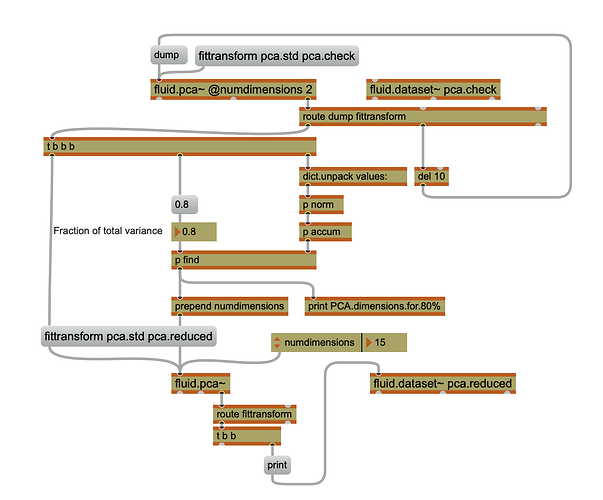
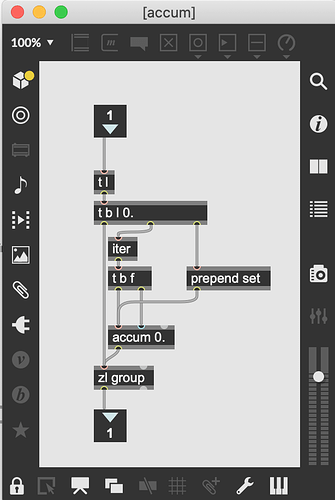
I remember a recent post where @weefuzzy shared a bit of code to calculate the total variance for the PCA. [but discourse search is not helpful to bring that post back to me… thus starting a new topic]
I have a standardized dataset. I’m now first running a pca @numdimensions 2. Then I’m running Owens calculation to figure out, how many dimensions I need to keep 80% of my data. Then I’m running a further pca with that many dimensions.
Is there a more efficient way to do this? Would an argument to PCA be possible where we don’t specify the number of dimensions, rather the variance we are aiming for?
Sorry if I’m missing something obvious here.
Thanks, Hans
1 Like
----------begin_max5_patcher----------
5504.3oc6ckziiibk9bV+JDDl4zjVSrxHBCev8L.imKMfAlCCLZXjfRhYVra
JQARppptMb8a2wBIEoDWURxL6pdYAnTEWi2W78Vik7e7gGVuM9KAoqW8GW8S
qd3g+wGd3A6gLG3g7++CqO3+kcQ9o1Ka8wfOGu8mW+n6TYAeIyd3rUaWss3n
wmyhBxx90SAtm75s9GeY8i4+d0eO+xB2auU8i6OHoE26wyGBOpua6aCe4ftm
o8nj7idxOa2GCO9xSIA6xbuIgGeC5wUXDwy7ag8+QvaPq96l64e9gOX93wAJ
qGBRS8eI3Fg8TR3wrVE1lEPRiBHoQAD2t.JMBiQ.4RyuonWk.1Rm4ojfSAG2
uR2p1GdH3XZX7wzQJunQzg1g7JvJiDJkTqXSTyg7lnaKAqdNLKKw+X5ywIGZ
WXerEAVfFQG7PXvHxFrhynROjhxvdTuGWoHyBetpju5zN+MoY6s+NIX+4cA6
KtAMuHM3XlellO7TT3wfcwmOlUUfFF4PTps+b7wrzveyd0XSWbGPn4ZO5evd
sq+gjP+n0ikMwcFDTX1FtRI4TNl6Q3Z3VwrHKcZIVOGcNb+l89Y9oAYesIHs
USkOGE6m0NaiMFDDORDj1NBpnhMRgFwTddaTJOAhYwPlRnQQO77ghZv6qshZ
QgoYC.0DuQnVtUrlvLm59TCYV2wC0gbWNl8jivNNsKMOq+JAR3bagmECYnMx
w4lxSLMtky6fEBzFNgSUJrTvnTtVQQ6xhOGtn0gfr5u9e+Cat3gdi198FI5e
ecCxIaDcinNB+PyfM1KK7Gy4yg+38AQZGfcSdar2jNM8lJokkJnpMZuuLrTp
jTotyUquRkuJIVafR2L5L7hVEON4h4qjC91FqWoTjnMQkEj7TvQ+sQAU6G0M
fvC5WpQn61T2viRIOrLsdLVgnBES3wDJph93JdkXRKZAgGKZA5SNgZAqN1Yv
ZMghJ5zDYplYzlJOScCBXe.AI4hXtLp6HCiB9TPhQ8sxq6g09mNU4vOT4VL.
yOGaePxGKOT3Q2gvkGJI3SgkO1KG1OQKGYZg3bhyg1WJMMXdNw6CRNdNzdSt
Cp6ixaS1dCiivzS96b2roSq3zWPFLR4LN3hox8+Hb0E3P2c+RT7teIXeEdpt
CTm0Q3wpQYV6z6Cd1+bT1S0bdS1z34eNuI13Iaza9CqeIIbe7QSinVeg4vEu
Nsv4BOmWUXrWwQ+SMbyZFmFWZ4joZg7b5V+DSWUtRKo3jYwwQ0OU48EE7bV9
oOEd73UnXV7o1OYR3Keri6car9jG55YaOS5SmO5N6SZRQ1So9epNZm4GEkqy
V+w+Eesk.+rfrPWW.AUdRmgqOltKINJpl75NymZ3L60r7cAeNbe1GyMtb4L5
KO7TAIZcYu79vWBRyperL+WRqejzre0A5UNz4s4ZwOkEb3TjVJpeAZ0CcXno
eL9yo4WXAQqJ.bobKU0pqZ.r1w6xPXcigeJ3KmRV8u8Ld0+o9Sxp+b5N+H+D
iN8Jb06noL25w.50FQIjpOvl711twzVCQzZOEScQV3hPjxK7y9PgSibiRSO9
8aQqRKcMOfr+uASv2AlP5FSvTaF+JqQGlslVDxDCI1l456hF3oZUjQuNZ.Cc
o7VlOq0B1EePGyaccXaK639fuTw20j.OtV95lAfxp9zZ.EsGecO5AtZ8LkHv
EGVFK.sXFx1fLmuYnIM9bxtBdQAqeU8Fm1zaV3wR+2+zESFqv0tvCg6OEqyi
IuofYXSpRXh6WU9eCjuO51NYfscS27JzL0JLJQCCAuEpiS16BpD8F2zHs2zZ
lJ9gpAWt1D.w9mbAK8jeVVR31yYNJZ0vkGkSccDla8itxSbS97+vkF2TkVh+
tcmGYdIT9jlWRyolIgDStjXB09+nBBjXBjXBjXxrkXR1pn6K7Rp7NhtZXYYf
xCxZVhntSrX6pm6DMpO.PsBMp6.Z5IYCOWlWRwFoGU+OlGUJQbppHb7kDnzY
i8RR74S2e9XLzzmOVdsMExagn7RgufPj1cYx8oXwvSuhUN6QG8AWRDTA2iiX
HtTZvqkFZJlACo2alsLxziPXJuUELg3svRTj1wzfLF0uAIF8N.L5frUqoOJo
fPIHthvPTF1X.msz.lMl99.rtAIb6Vso2sdGYiY73I5zkugUkOd7uipXDeVq
Xj4GVt7yn+Nn9QdyV8in3F7Q8tuZR3gVvA1bVQFSbmCqUPmyVg5lBl0bq.me
gyWq.MzVwbgEEc281J7lSdAan05jNqXAYj8HcUwUlcxoPPMDQBwNSOZ3bykb
QeOn6aaECQqqAxv0nKh3JIi2FNm4wDLAmIwHJ0ht7FO0bJVjgHVjYDb4C0XR
gE3ucKcbgO2qqc7+Sh+NSibU7yqxhy7iV8I+jP+i6BZXZcovSyz5hK4sVy37
4bMVMwSfsUOqCun0Rjalf8MNEu7lzIrmjpiZlyobkviyIZUQpKGVnL4kkI2k
DAE4AkIGJSNTl7YqL44SRxU3gTggGqah7lBMLWk9D6l.2Bukt5K+G0mCSc5v
3lhNHl9Yqjxg.lbokDlTgb+fKmv2KH1TLAe6Ce5gzvoyFqQJ1f8XJgr.lTkq
7gEDmtLC49ScOC4FQ8rXy1DgiqCMAoHZXy9izSpOn382b.i9s+b.60.OroGd
HNivuN7grX03jO803L25qYLmzVe4BmJhRv98PMNGXNvFSKyWl3CsLGFemyWq
fMTrXNKzZgH1ewE4y4z.bnk+BOmMB1XHm3ukKPSmqU78mObZDKX71VPprl2U
.nic0UlOm+7DraWy3DAcVVidg6x1nyhze2ur5S9QmCR+iia9NxXS65vpoEqG
Fqlk0Ypo6ebRKeZJakmywmGhe0BXmgW1cF.sd2teYbP.lRdiV1+BFuYTCKwK
zx9ua7ZXK5+KKI1EeQ+ScK5eOF41E8OSNuK5+U+4Z6CIqHuxcA.b4reZowwB
s2lPQ2Bp9tQQie0ygCPgzbgNbuoM2kpKsE0DYe1M9AJcNqWo7wadyqw1TqGv
sCAtNXlbb3lfXj0Ffz1VRG0hz45gtSpyevzDQx7seF4FEUz3QTb9M8lJlXSK
mrkd2AKa0hauEYSVYL7t62j.M.TTRmh2jn5XSNfkfyc+l7jCgYPmp2TexDiM
Uuo9XDdhI3MwFhdkmbBdSxgv8DSgLYFOw9Y40aN0WYS2OsWsTBoftXvoX.uI
NYo5375zHufHMF4kdhMLhvSnjR8uz4KQzGTvsSqxFN4s7.zqSRFRuCuKAQ6g
wHHBcldMjBDOeqooiSxUWugXILwJe6IlBKH8ZqZJr+ZCxqeCvSASjOHyhdSg
AX1.dSpo.9TCgSR4SvahxGJ5ges8SC3EgY3of7QI246xE66UydDyq4pYMxUy
XjFlsHsOSQtdVhXKTma.yuJf6Ko6bdeX7+mc1N7zOFb7rKyfh4jQczX6KOGF
EsKNJ9lYKSQBIqcmsbhoTbs+zJzFhhgwRMtrghoBhm8a5uX1WctTuZ28fKtI
FmoPDykxzlnYb62jDJmZ9F5paib4cgvJ2a.ojHl6a5CYVfAUuMc544ytCQko
nvoj3SwIkSykMTU40eNK9kD+8g4i3.pVYHeLmLknO60ySg0Gz.ZXw8Tk7U1Y
7+5eLEgxyBd81yYYkyxnxtfZPpDQ0YeYDNsoejYtch1nxE3pywoZ2jPxnXKh
fYb8EaARMhRT42TUYQKs4.zz1HPOV4ipWUPTfYzbpcwdEMSOyOB22brgaZv5
rW2VNatZoAKzJn1FrNINjCJ7HJOiPTsoXpXg8FeJ7nQqMn2Fept0amieUde3
7Kp5kOF1BtM1xO9iH7S+0yImhB5Rqszz1UP5iW8oTUJFUmlV+TEqcWgiXJFS
IkXAQpUUwCBBufI3qgvx6n2q7JRMQhsTOABi3XauqRQLrkp2zPrgUpe2rIIB
hgtH0bLSQtxnRcaQ8CS2XnbhMdUeTapVZLyTBrG9qQ.z1F7tPhILEVUGV82s
6ZkVgNvRhidgc5r56hf48qtyXTjzdGDEkfr8kBtm9sN.0mBcfgZy8i0r41he
u5pNdLlmynAU2m35njRrf9ZMeLLd+8SgGMAqNwWV5AVJbK+Sy2LdS5j+2m06
o1Ubyz79Xq5XSDNHg6I8bQWvzho5NLY2GYqXR7AzMftsHzMfvADtElvATtu4
obn2cTNfz8sGo68ByB3VfAs2DZGP7.iZyI6B3Wfgs2BpGTyMf18FP6n.sCnc
KMsCr0AjtEmzAV5.R2xS5fzI.Z2xS6X.oCpQxLvrf.2.iYKLkCBaCnbKLkC7
dBdOmCdEG3UvzNZgobP9m.oaoIcd.kCBYaIobPZofMtkkvAtUAJ2hS4.RGjX
5bwr.tEvslEtEDaFvqlCdELt..uZN3UPw+Ad0zyq.qU.qZ5YUfsJnPqKJgCF
ASnpWKKgCpKAP4VVJGL5kPnZSNqBAjJvJ1Bx2.ulfQrImT88Qo7WJ5w3Xvyp
sm7a08W57mp0S1ADGrOLy7m.mq2OgYVzxtEJmuwBOjCM87UXjm.etKn4QXNA
ADtklvATNnBvKNkCHcPxEyEyB3VfAs2DZGP7.iZyD6BxCEXVyCyBlUQ.yZNX
VfEKfWMG7JvdEvqlCdELOHAd0bvqfo6HTP+klxAEh.HcKMoClxiPQWWTJGjf
IXiaYIbfaUfxs3TNfzAIlNWLKfaAbqYgaAwlA7p4fWAE+G3UyAuBJ9Ovqldd
EXsBRWbYIbP.8.kawob.oC7dNWLKfaAbqYgaAUn.3UyAuBh4G3UyAuBpPAvq
lddEvpfzEWVBGDPOP4VbJGP5fIm3a.oCnc.saoocPcM.J2BS4fRd.TtElxA4
sBTtEkxAqhSfvsrDNH4AnhuyCuBXVfwrklzAokBTtElxAokBTtElxAokBTtE
kxAa5F.gaQIbBfvAid+hR3frUAJ2xR4j.gCJ71DypfjQAiXKIcC7ZBDtElvA
TNHYzEmxAjNfzsrjNXjr.B2hR3fTG.B2hR3fQwBHbKHgCnaPlpKHcClIu.ca
AoavHzCNSWP5FL97f0sEjtACUJP2VP5lBnafyzkhtUT2sqeL4jww9zfQp.Hu
KH4sxPiMYDXX31.R7RShggaCHbKJgCFtMfvsfDNxD6jdpiZkMwOO9j97JZca
Omk4nEspqJodbW2pBQwLGMjQQDk8aMo4Y52oXpkmR8zT.6siTZBhrAtPTv9t
sVv7zlIrpJDrPXerRNiqnsp6qYiFkJqZIlUn8fHTNQU+lBhBNbMStO0spMds
BTtN2k1+vLB0zalR3LqjRKazTQwwXz5u5cwGNjq3V4cGE3mbcCPiWHCfX9FQ
a1gXAFlr9y6X79fz5Oslr.LF0XbOzvx3hAhHPDeaIhkTwiAeNd6OOtW+gfzT
+WBF2McVCZmG2szHR22Mc77gsAIKOdBH5jhnD.MmPzjBn4DhlL.MmLzj2AVd
cHQRD1y5RVv4TW9nLAVYxG80kG8XR8K2ytM8OatsXEAyEMEihtcDrOLaoEp9
hS5NaA0izrMnbzgWg8FfBx36Ru+hdTV9BpPGDM1UslhnZsePnsU5htJTBZC2
6p6az0WYAJ4wq1HRy4ryFocghYDkyjzW6jAikbNlX6Y7nBpm6aHOh8ab9qUI
JMJb+0lEmGknpu0W7CO902ZM2VUAX86438f46TsTsynYLtrTqJZA+1d+cyPG
AGKTbuNo.M32+UUj3Veoivno6rsTv2ggCiwp4s21HqOwhazL7XTPVqUlP+hv
FkJa0Mzt.QV6Vpb8raX.wmy59oog.haHEXkUX.kWs8AFQx8YPmORC5Ey4PMC
KKHQium9XOJUEZlx7JXoYUdl5oX+FqEqalwbfWmJwcgZf60rfUkfSM+3hLw7
vZ.FODj0mKIcmLl4Lbpa7TamLk5QL0j6lmWx.bvnndZUJKWI2Wmf3wKebiWW
ugwznW02q4RCoNlCzzXSMmgM7Q2QE8H0Ek8g6x17ovfO2sjX5QcZqbNx49vi
n7HjFPmFJpW8GFQQbAEpPdTtyLlTvEhgPTYkJ8hBKHjbaI8ALLMkfjqVnDHW
0jodJQSRwA+rjvurKKIpCQoaZVisghtDN1zo3ZLXtWika0XHVaNN97ow2FpY
EKx+W25mzwCAo3LosOAiP4TU82HkNTp83RBR6vvLtc+wMvz6fsd2QnguBGy7
21kaDs2VjbLchixXQ5t3SAesKmhkCmJxnziGy3FzJDbMUZen+UD4wEyKeH9E
8FoewhIG8MCGy8GwZyMLwHaXpuqbXOJ6h+tzg8PlpJyWNZCKGzInpM24jNYX
lfemT2lwqMzNGZ.tNeChOp2jjfPbfPbfPbtgJMgQQLn44fAjJbfKKjJg9A5R
9cf4LNN9hwS56g.65YVmoJmQ.PDTeiDAE3GD7CB9AA+fem5GbzN.IfCPvAH3
.Db.BN.AGfeO5.jBN.AGffCPvAH3.Db.98nCPF3.Db.BN.AGffCPvA32iN.4
fCPvAH3.Db.BN.AGfeO5.zCb.BN.AGffCPvAH3.76MGfXTW6SnuxUQgVDvRq
YQFRQc9GYZT2ssjvGzjZ8xPT1u.8ym7y18wfDDps8L5A+n9Emmu++OFlEzEB
0yV51jzOEE9xGKHhCekxnCyP6ZwRXTZvWj+MgbPazcEdw3krXZaq.76VtN3+
EusweYvxzU.rtw8JVtOMEkg0rvkUtZdbZSq.6V78CiQYVHvNycUMmjaNdZaV
EapMSpwfIYwRUrSKd625XwRIjRMx8Xie6czpkpqtu5ZGCqWLeyXXnrK29DUo
tNSKyzIc2A1dEWrF+1t.+ds6cHs3Pd521P98vtK8X1JTWrcgt6Z2f591xQZK
1vduuqC5+91aSTiVE7O79PIb5Vksfp5DopdOIxccr6fJ9DphOXcaGp+eEcNn
as6lRXcL6wSuxF3eIIH33nagCslmuxF2eKHJJ9yc25tpCjrAwUHjrybIHbrv
E0I1UBK88vaz838K.1szt+Rbz9QCthxcecd9lCpoxZUL2MIMv3je1+3J2MNb
mOJgB613g7nHOoiYhISqmGpf4xlBQ4R2lWOh5wXuK9CSR6aN7W61Zv6kDSrG
no0MiTYTWrczXNNup7dbulqy68xFcEHtmrQZZ+m3wJeLgMmyImFkdAEwx+iq
.gi7TtZAJ4dD4.UMDk6yqLr4OILOVodnSmbkDrKH7SAoiDkuveuz3PskQw82
3bk0yXybDHeuVKaxDSu69iSh.kFbbe56MOqY9oYAOeNJJeycd3HcWaTtshzp
xgpvqzZqYzSDx4PnFsLQzFjc+4WhVh4ThhpjuFY5Mu5setuRiahZ5Y+cElep
3TcX+cP4UuM6R5NuHRYkdIk.FI22oQSu1isPr+oUq+gD632bGnn8ItdWjeZp
44kdJGcVapy2G9me3eEo9glI
-----------end_max5_patcher-----------
My understanding is that PCA is deterministic, so the results from your second step there would be the same as the first step if you just kept however many dimensions it took to get 80%.
Yes, but how would I know the number of dimensions to keep 80% without calculating the first step?
The two successive pca processes work nicely in tandem. I’m just musing about efficiency and whether it would be technically possible to tell PCA upfront to keep 80%, instead of specifying the numdimensions.
IIUC, it would do the same loop that you are doing under the hood…
I agree that this could be a useful interface option. Internally, not sure how I’d make it work yet, but I’ll squirrel it away in my desiderata bucket. Meanwhile though, you can avoid the second PCA by grabbing all the columns to start with, finding out how many you actually want, and then just ditching the excess with fluid.datasetquery
----------begin_max5_patcher----------
5980.3oc6cs0aiijc94t+UPXrAIAwiRcuXMHOraBP17x.r.4gffAKLnknsYO
ThJjT8kYw1+1ScgThTl2EIcOSebCXqljEqy4Temq0E82d+6t6wjOGlcm2O58
ydu6c+s2+t2Yuj4Buq3++t61G74swAY1G6tCgeJ4wOb28takG94b6ky8dz6w
xqd3z9jS4wg41lPJt5wf7suDc34GRC2l65RNcC+dOLkuAcuGGqL+gP1f79qE
sw8Zx+xwPWCt6wfCOe28E+87iEsyRDZB6GnrJTQzgRh.at1e+8u27q6GHqtM
Y+9vC4ulWeI7f21WRN5k7jm9+3kcJ8X7oLuOEk+h2tf7frv7+uSgoew6eJ5v
ObLNXa3+b4aIN5P31jSGruJZonIMLS2SA4QIGdnwmntHE0tHkJ8sBSlXCAwH
XgPQjBpvWKm4HysXxJB3pRN5hK4dJI0IvB9kPivKH84SlG7d8U9h2WRNk5Ec
33obuWBx7nHusIwY+n2yoAO58OFt2KHN1a0jiDqvhnkVRljS7o9BI1WRj8KH
wKtfbuQ.l8kCZgYdzVKl6twxgbegU6SQMLSAOY35F4IzrwS6CyxBdN7U7zwz
nKbZct.2NWfYXCWH3hMXNWpjJNgyQXeMfmR52fRiFQHhF4VxD31VrW9T7onc
aJrU7UuiaC1jFt6z1vcMKAJwuOkbH+PvdK0e2eJMJH9t9kMJxFejfR3HpBy3
Bkd3VfsxF5PL19TbRPt4CMKrZwhaEJNK5WsuSrt6lOYXplfC8xSCNjoMrrez
deJEOZ+NbDmHQ9BtRa3zWeQEZ.PmVkHzUE9Xc070twMMo+iLbO2WCN3LIiJk
JJWg8oZzAFMbWw8fNHKtgiswgAo26EramFJ7bnGx6Ofu+BtnpxU+JZ3dEXM3
YkhYS0RC92EVZ3RqrQfnaTJgDw3XtfvTxY0RCVszVZZCh8TZx9GO8zSgoVAn
QZp6Vuo4xhKjFgEiK2fILtu11Liwo5eabCOUeV32BeVY46FucmB1WYi5GSHy
koF77E5eKRfODkuI6XTb73yzw25qgxnaXJeJmP3Re8nuwWCCeC9ZvyWvlOdJ
OO4vDMKpsJdslO2FXIueE+l3K0EqMoZqP4goODdH3w3vpQ0tTiywQY4Oc5vg
v3wKMJFn0+gJoRASGes1sJ0nbqiQs2AZSW2n.QtzfaSJ7QSEXSDMkmDaDgQX
rj1DeKVZ99zuF4gQnwaGyU8BBQsQytXrPC8wZVm46RMbTkxnCA.aosqarpcH
IJKzC6YsvRIdTzjMwg3aDZgBCQIDhNuLjvDPIueAhlNdXePdZzma0ZGcoACG
CC+kud1G+T090J8az1.wRAl3qPZ6gDSYtFP8sbd3ZLRwFYc57w5t3atv7d+w
rf8Gs0goU0CRut44TW4E7ECk46p5d30vH3D7tacARIhMTDFwYXIEqP9JyntX
D1.a1.n+hmAEZi+Dc6SEjMJsKecrLbkzWPoZ69ZKh7IECqPtz15rQr68W9O9
Sa1EsO7PVTxgrM5rD23i9GFcEzbJ6bjlc457.UZScXgOVZy5w+UC6UYz4KTU
sRi9czMj0jFbfknEEWQ2oQ60MyvfaP8FbGUmyKmHnbFknjRs4cCeOrvVqqLq
o8xNFetiqHY3j2x.+N5cn0JI0UQHUNWeJ0FAhfQ9TlPGAnzTKElZhIzoncls
qkLBSK3wBlTOTGEG9wvTCvtxS+t6BNdrxkeWklXjLeHw9h7u+7khN3tD97kR
C+Xz4W6kKGjpkF4ZQwoTWsB97Yvs48jrKL8vonyiS1AoBZxNbXpwP1wfstFa
F0JucE4KR4pQsqLKt+m1fyEYpd7943js+R3tJvDsj9X3gnCUmVfZ2dW3SAmh
yenVkCHaZ79OUPhMdyFKTx6t64zncIGLDQswBykK6NMy4xClWkYrOwgfiMzX
MzPKWZ4lYZl7T1iAolgpBcFR4MySRhqeqysKN7o7haeLRm2ScoXdxw1uYZzy
uzQaeLQey8c8ts2I6gSGb28AMnH+grfOVWZmGDGWnzV+0+4.skrf7v7H2P.A
c9lN6FujsMMQmxdU90cmO1vc1oQ4aC+Tzt7WpYbzbG8iGcrDDc24Q4cQOGlk
W+Z4AOmU+JY4ewIzqboSOVnE+Pd39iwZtn9CnUOzoCl8RxmxJdvRfVUAvkIv
spVcUKf0tdWVBqaM7ige9Xp2e3Ir2+p92Dc.gaChCRM5zd3psn1TsQpbiFsf
1guFihPQ.iHaUQnUUK511YqUdtk.JdWoWiBiRyu76Wi8xN6Ztc2ys5UwM+Ut
5jwdU7yCnPQsVs4kUjXeq2cav.WoCnm+8DAABUqbLpxMJmm0pZe12zgcgeth
uqYQ73n91kOnAolnHcHfpV2HTqR.7sJAt3vxXAnEyPVVvb+lEMYImR2VNNVN
j4UmczldyiNb1+8OeQA+pGLIcmKjngMdsbjFtcRCsHjVCBilIMCdv7fKCUfG
yXGt1CtOZ2wDc1YY0lcVLw8mJ+uFo8hKVFb4cl.H18fKXoGBxySid7TtChVM
b4Q4TWGg4iAwW4ItIe9u+BwMW4kDrc6oImXRy4u4OwDSnbHwjlSLwUgOpj.I
l.Il.IlrXIljetFsSNKCTQTTCLp51hth52dzUqSRFlJV+zjywPTTcd4FeAU+
OScq7QbppLB79kM0mb9VETp2ZAkNarmSSNcbxxphBdJ8esrhymgryXn25DV0
tKSmrhUATRf1v8IRpjK3HFhaVHlD4Mplwvu0nGsqZsOscdY2PlsEKz8F01j2
rHh7sfknXsio1kOzAYZViVT9RBkf3JBCQYXi8Z13rF0uEIF8sVfYiouSAVep
bjMRyLsoSN5U.JAdXBrtER31MaS+FrhQleXEBAFcFpeD+2q0OhhavMV+USR7
aspIwGZIaLQxsX0EwXqwiL.pfQVZp.ODp30kw45pyfHtjCEa3blfYV6WLeLh
pU5zo+xa7VKIaMjgX1RV5K1PK.GV0qvkwbKfBTCwIP1PZ9dKEeMzR5QUKozE
MPpPrjiwT0HGiWNp.OTp.uTTg+P05nKnr.qtcc+emT5311qf+moAaMDoc2pl
jGD68wfznfCaCG8Bdhxr0LloM9fUHpTwjZ66JphdYw91xFHTs3KcuidOoCuX
pKecscUMGgEDNVwkDgIt5As18ZccK2x9w.pRtKyDJR.UIGpRNTk7EqJ4EqwS
O7larjmXjs3TRwXpnvU6ng1VI2uY057ewCO4BNnbRBShx9DluB49A2zReteu
FuplCx2ZYS4hz8FgM9xMXASI8KkOlxRMvJka2Xk8Hmnu0xoKKPt+stWfbSYF
p33M9HEQK.s+3aOBOFpNX6BM12cKAL52dkv61DODm834R9vlG4C4amRbVXe1
LiTZ6yboSCRIYCpDm7eqsf4XCLGXit+hUO.wPqBGdAKGfw04vJSDeIohAOfr
jkFgOzp8VJzVlBzLFrI56vk1m6TrY2o8Gm31Nj3q1Hpd.1vDly7ma3LEfQV5
sg2tns4azoLFr8W79XP7ovrebxa5pl1AhX7T20UL1huaKeJJu9gSSVdsCll6
6.Mfmzoyhaipi0xKcbjbp8HZvbEJq+ilkl2GtTRmU2Z4NzmlxgPxTNJa3R7q
OJaJNPwliixFzazglkS9oEae06Op65K6B1V2x+za.x4NMavEmlVzdO3KFvY7
BdpBN6qqdbWN430tzJjluxUVsoZnsIAqharWMfMzNhxp54tsIzXt5n9XIqt9
M2U1AtKSAdOS+84cobs4EszdkO+0mtBEkp+025Fo6qnnVhlzeFjPB+gzSx4p
m5EeMG.LBc.7j4zV714IwP5oZQid0tEZ5L4f55YQbRFfNDgNG8DdH7zbXXXH
15vyABAOjgI7bLLIF.KULRdS8ibHiQygjiRFjnCOSvg9P3yAZXHFlvyACgGh
ljblPc8FdxbH43CwOk3RollbOoFxfDkOGntgDHjZNjdbxPkdqhGw50N75.tb
AUwQ3MRhOiHzAT4qyHhHt2Sga4Vu16J51XigXki+Zybtv8uZcSX5jqVuDWsV
IZXcRz9Zj350GgsDUtoJ9pbLtj3zocQI+2144+geJ7vIW1LkqFg5xhGe9on3
3sIwIuZchTl3zct6ddIYT9r+rGZCQwvXesbYCESklAM8mzefyqVWPWavkMhw
YJDw7nLAQx31O4Snbp4SnqZF4RegvJWOfT9Hl6S5KYV69UalN63h00frxjye
LM4XR54E3wFp57yeJO44zfcQE0ZGUq.b2W.kR0285Yn+t8ZAZTYapB8NOX7e
EbHCgJJkQ44e4UCA0Do9HphXkN9JymMeRUvvUXy5iCReFEakHXFW+vVAoVhZ
1Dt1FUkWzbag.5lIhv3PyLTTqshRBPX9Q59jabtU5Gceke8JBVmF9imWGSsP
vRcrAVBVYNZ1shBAQILLQ0dMSSw1kpVkViK5zpcekZZXexGhNXTxCGFA2GZA
2FZ4m9ID9g+h465gvaUq8LhtYkPBh4zAsLAGyTjqTipq8goXcLZmaf1frBga
pEKl5Z8JzGrc60.OIk6f.BN1g6TXEAeEt6JfS+7UiXFSC0ZWhK.GSMAT8qcv
XTjuk3HJJwzUZBmKzMtdaqtfx9YuVU6I9Xqxozbn.ZeYJkhX39A.iu.7wsB7
68IO6j8Ji.2e0u8U03sJqtMTepOk5.C0l6K0r4NyZPiFeWWuy+rKOcrL1ctn
4SFy2cp9MLipymuuNzxzd7kN9lK7ENe1LMun5TOSHXLgyrLUKibu.eerj1pa
gg.O62tbyXtQaxtOvV4pMCfa.baUfa.fC.bqLfCfb.jqcHGZYfb.nC.cKExB
vV.15MvfF.7.f2RZTCvW.95swvFTyM.18F.6n.rCfcqMrCr0AftUGzAV5.P2
5C5fzI.X25C6X.nC.cK.xBBbCvUqrwLHrM.xsxPNv6I.4VBbEGvU.tZcW1Qb
H+S.zs1fNA.4.H2ZFxFjVJ.3VUabvdV.fbqOjC.c.naoPV.1BvVKB1BhMCvU
KAtBlW..WsD3Jn3+.tZ9wUf0J.UM+nJvVEfpV0BsByfI.3V0pdAyeI.4VYHG
L6k.fa1QUH.TAfpUzJF30DvayNnhrvGrpKL7XbH32Zrf6Kb6Gp05N.Eqoopx
yn0cQ4luWgt97DlYG7rGgxEGrvC4RyOdEl4IvF3J5yEVSP.fasAb.jCfbqYE
fgkJD.5VljKfirT.a81YPC.d.vawLpA4gBHqkAYAqpH.YsDHKvhEfqVBbEXu
BvUKAtBVGj.tZIvUvxcDvUqbA8gE7H.5VcPGrjGAH2pVzUHAS.vsp13fEmA.
4VeHG.5.P2Rgr.rEfsVDrEDaFfqVBbET7e.WsD3Jn3+.tZ9wUf0J.UspoKBe
SgAPt0GxAfN.zsTHK.aAXqEAaAUn.vUKAtBh4GvUKAtBpPAfqlebEfp.T0pl
tHCBnGfbqNjC.c.nacWbhLn3E.r6s.1A00.fbqLjCJ4A.4VYHGj2J.4VUHGr
KNA.25B3fjG.H2xfq.jEfrVaiYPZo.jakgbPZo.jakgbPZo.jaUgbvgtA.3V
U.mD.b.faMm8dIjsJ.4VWHmO.3..2LipfjQAL0JZDC1Hn.fasAb.jCfbqYxn
v9CE.cuAfNXlr..2pB3fTG..2pB3fYwB.bqHfCfa.baEyTEVIu.baEgavLzC
vsUzYJL+7.baEstASUJ.2VQ3lBfa.basblVV2sqeMEfww91fYp..uqH3sxTi
Ma.XX51.P7ZChgoaC.bqJfCltM.vsh.NxL6jdtiZkMyuO9r99JotsI62W.Eu
nrtMNLH8ZfgVsAYzaLehnUjHVvEyu9vZb3tqU7qCKYBMdz91HXozpX4yYb0U
vxv3v8WqILLcx5VMrZ5VJEyJaNhP4DUCKV4GOkm6TYak98oBtSaTgzuXG4vn
HhkmDMSDHMMPszKUn0bsMGoz509MPDZ6CElTtPDMIMnDNy1ozyLFUVdMFcnJ
3U65CI6Byp2y2pZLtGX343hAfH.DeaAhmghmzr3ow06Mhd6qQGNs+wvzQ1lv
Ok73GFWa1GlkE7b35KOAI5rJQIfzbFklTPZNiRSFHMmMoYYj9M12SOQ5yoDS
kZm+XWBgkAkX+Eg1V5vck7MZCWbU6FcN6ybZzye5pMgcdUx5EgmZSX2VxArh
f4xNyS22GgE1PkjbN0IrziNJivZYy.27FC2Ek2cXlyO40WLlSjBFcno31BRt
SJdRVqZNmc1HsKHZ2F6PrJ3taKUIaXB4wXV30MajodM6VEpQDbrTwEso6L+Z
aYwQ6t1g0DQ5i.s9bPzgutbpWs5HgMEh04SuaxE6y4XhsODTIU39DRPrehyu
UCRg+5tfsec9GlZAt0WHMSrqyziVaMZHiqDDKF3O5Pb30k1oFPBaPR1BWnMN
iriupBv0qjSImx69soMtPbE7lct7Pnhh+iGlWvoYPmORC5kq4vzlLNzvTALz
g+qPMJpP+3VYZgtijH3lp+bKvUifqo5T0DcOr4fY077yHWMZlFlcMhpA1ni2
4jsThau9XcH62EsMeyGiB+T2VKjXla7Vw4HWmJHJAgzvqTG+PdXp164wW5w7
WIu6WT3P8vivTPV6mX8XCxxRbp4GWLXFrQWt2L2mWOBCdEYd8b0x6y8g1PiV
l3FCwXpU3PoBxYkgdpBYyLE6rAGYo0KRgcr9.FLsZFofqTRjq3sTgRR5Pn3S
TDWlWJjfxcgR4K4RYSRkf7znOuMOMt+R4dFWywFjsirvbQGkxcP1J1EELfdu
8vI3WY5I3w9eaSxMsPG6JxuSdIaaxwvudCbSaxQ54I5EYLWh6bFBLQ4pi0M4
zwNbDNfQliwAe4wfzNdIHEm4aIFLBUHG0ehbNZ898KJFoewxEG8qlCmoOiJM
SXxQRXpwLYUFHXowK+xATol7bFftVEYdW0D255eXX959FobOM3qt6z6l0vpG
sKsYHoyZlB9cdzicFJmDBk66zP45MxodBka1hFaTIuBQi86wnwlw.U9scfc8
rpyTia49LtHn.+ffePvOH3GD7CB9AWM+fi1AHAb.BN.AGffCPvAH3.76QGfT
vAH3.Db.BN.AGffCvuGc.x.GffCPvAH3.Db.BN.+dzAHGb.BN.AGffCPvAH3
.76QGfBvAH3.Db.BN.AGffCvu2b.hQccNgd83D12pLwPJpyRDSK9cGtF29l8
t4E05konreF5CGCx29RXJB01YF8feU+hyy8+yKQ4gCTB02wn1jok3nmeozib
maOo5CWHk1lo0pfRObIK9jzWMjiTuRqk7ytyosY2bx709fOKdL4ycwSMEqj0
q3k83YgCqVCS5pgEMKM2.0QwvtMe+P04XE1hpFWUgMu4krJOciV5s+V4Iz3q
+TGa+MouuVNbeie5au8+1LgppqcLrQwhCigghtbmORm00YZoDUMqHKySbwZ7
jgUccX4zR3Cy+4jy2LmA0C7.O8api1plRnbQNJ5l1IHxqBT9a1Sut5a84gqB
9CfR3ugTBGUdRUB8d12ZyfJ9a+ATYq51NJ7eO9TX2Z2MUkswTYjaj.+yoggG
FME1UMrlQh6+MLNN4Sil57I5D8cwghcYpi35j14cp1PLODB4OWLf8HJ6OmDu
azju77ANNu3PwzTfgJVemEBLI8CAG7bM7auuMRZ+KXiq8UM3SsiuUc6njJr6
DJRPQBemxNd.GHR9JCP297XNtnL2BtPQ6pZxTIykpJhx8cGF9HpfMOGRoSFM
5l+gdxFooCuj6q7qYjbNkdrO8hqJnCq36S.BGITtB95yED+AJWkmOhfYXyWd
M2WY1rlO9JMbaXzGCyFqA0yZVWHNTUj87Pbtx5YrYNBIeuVKarB48ctpNKLT
V3gcYeq4YMOHKO7oSwwEGnvCWR20AJZqRZ044CPb1OfY5Ij9KASMZdhncU39
hhhdVlSIJpxeFJD6am73S8UZbSvOkO8O6c2eJ0N2V+018sQNWTWxY1lT3l0n
5Mn56dc3WOErsz.37k+CYZRQ6q6tswAYYFAS1wBZ6NSc9d+e+8++.5f2TlC
-----------end_max5_patcher-----------
1 Like
thanks @weefuzzy for the in-place crop solution!
Just a quick comment that you might want to increase the list length for all zl objects in the variance calculation. I ran into surprises when my lists used many descriptors and grew beyond 256 items.