Ok, a bit of a bump here (4 years!).
So following on from how effective creating a filter from spectral moments (as outlined in this thread), I’m having a hard time figuring how how to create a compensatory filter in a similar way as outlined in this thread.
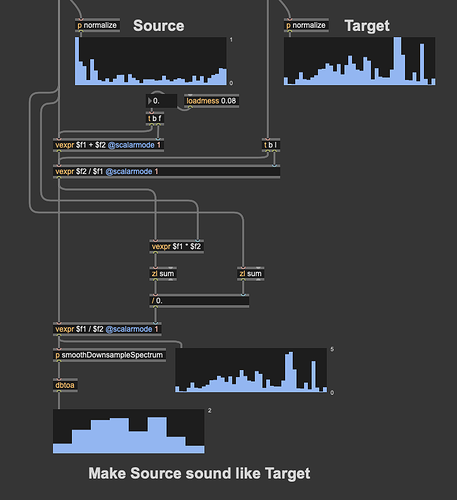
As a bit of a reminder/summary of all the stuff above, the idea was to take a filter contour (from 40 melbands) for a source and a target, then using some maths (from @a.harker) to create a filter to make the source sound more like the target. Like so:
That’s a (jongly) kick as the source, and a (jongly) snare as the inputs, and the filter at the bottom is the filter that will make one sound like the other.
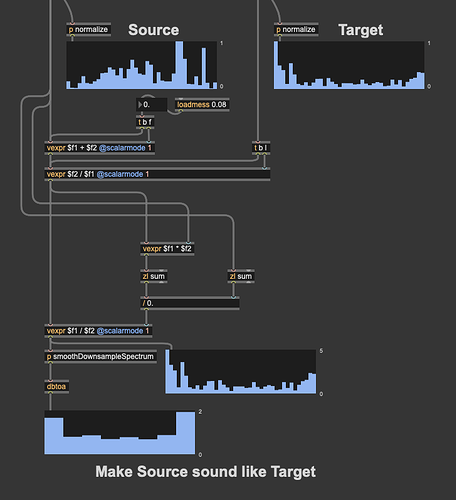
Here’s the same process with the sounds in reverse positions:
So what I’m trying to do now is a similar thing, but using spectral moments, which are in different units, ratios, ranges, etc…
Here are the same sounds but visualized with spectral moments:
If I run the same numbers through the code above, I get numbers that don’t make sense, which I don’t know if that’s because the numbers here aren’t normalized or because the numbers don’t necessarily translate in the same way since they aren’t individual bins with amplitudes being modulated.
So unpacking it a bit, looking only at centroid. If I want to have a sound with a centroid of 60 sound like a sound with a centroid of 102, do I need to apply a filter to it with a centroid of 142?
Similarly, if I have a sound with a skewness of 1.1 (tilting “right”) and want it to sound like a sound with a skewness of -0.8 (tilting “left”), do I apply a filter to it with a skewness of -1.1? ((-0.8 - 1.1) + -0.8).
Or does this need to be worked out per column/descriptor in some odd perceptual way?
OR is this not possible at all?