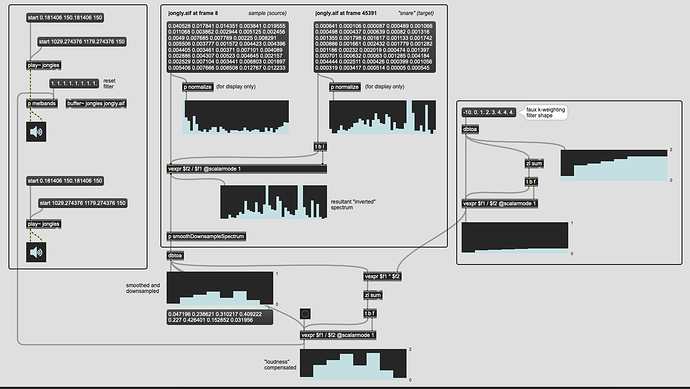
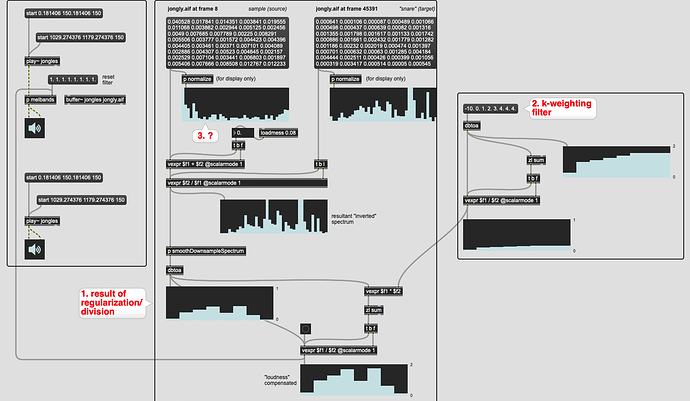
Alright, had a great chat with @a.harker earlier today and I think I’ve gotten it working.
It’s possible I jotted some notes down wrong, so do let me know, but the results here appear to be working correctly (barring my terrible k-weighting approximation (more on this below)).
So my rough takeaways from the chat.
- only normalize in one place (if at all)
- if I leave the initial two filters alone and do the process, it will also compensate for amplitude
- the resultant filter will modify the perceived loudness in an unknown way
- if not doing anything offline to reanalyze/compensate, need to come up with a k-weighting-based compensation
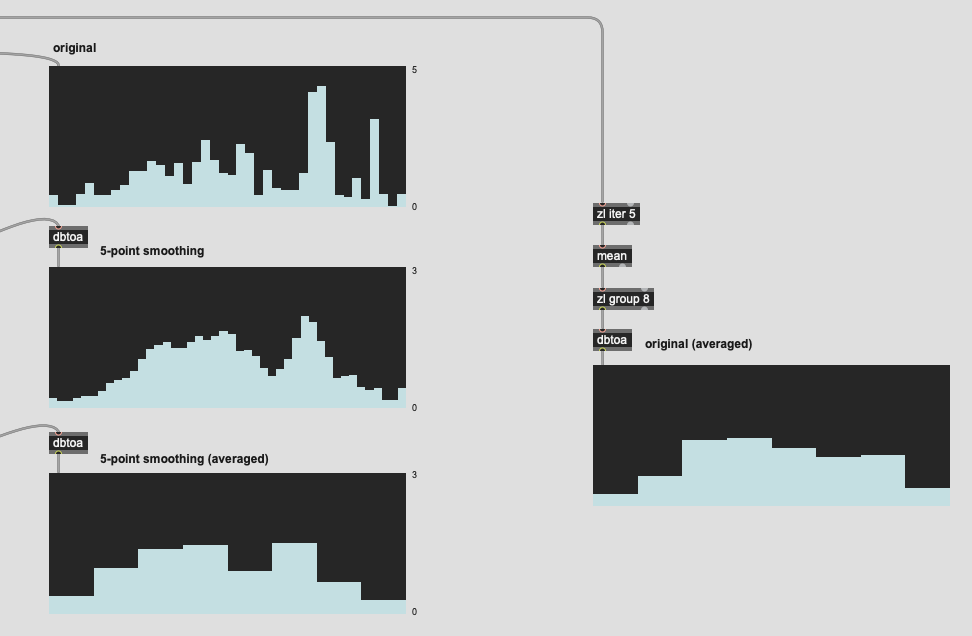
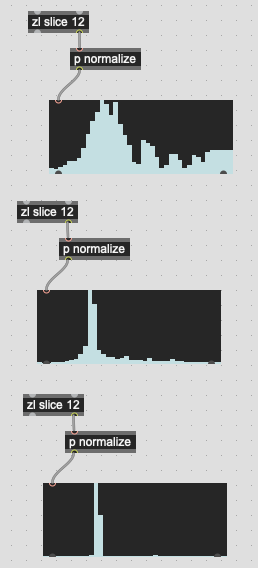
That gives me something that looks like this:
(code below)
So I’ve removed all normalization (and regularization) since I’m normalizing at the end, and then compensating for the loudness change of the filter.
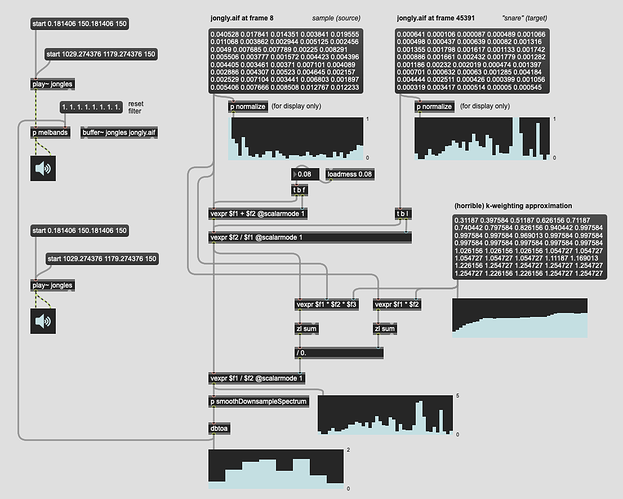
In my notes from what @a.harker said, I’m suppsed to “multiply the weighting filter” (created on the right) in dB, but if I do that, I get astronomical values (e.g. -37.025 * -14.351 = 531.345775 dB(!!)), so I’m doing it in linear amplitude.
I’m also a tiny bit unclear as to what happens at the very end in terms of loudness relative to the original samples.
Since I haven’t normalized or regularized anything at the start, that should give me a filter that will compensate the amplitude of the source. The weighting filter just massages that so that the shape of the filter I apply ends up sounding the same loudness as before I applied it. Is that correct?
So if I wanted a version of this that I would I would have independent control over loudness compensation, I would do the same, but normalize (via something better than overall mean of the filter), which would then (presumably?) neutralize the impact that either filter would have on loudness, and I would then independently compensate the loudness however I would want and then apply the k-weighting filter compensation on top of that. Is that correct?
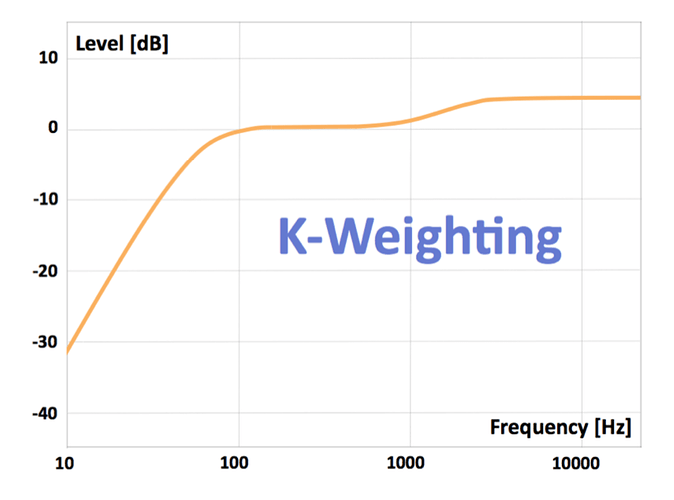
Lastly, the k-weighting filter is dogshit here. I literally pulled up a google image search of k-weighting and eyeballed where each of my smoothed/downsampled melbands would fall (371.274232 753.952319 1269.088749 1964.959113 2905.690638 4177.751245 5897.994634 8224.419765).
On top of the fact that I don’t know what the formula for this filter is, or how to compute what the gain would be at each of my bands, my two edge bands are shelves, since they are the bottom/top ends of cross~ filters. Meaning that my first band of 371.274232 includes everything from that -30 dB at 10 Hz all the way up to the 0 dB at 100 Hz.
Is there a way to calculate/computer/measure how my actual bank of cross~ fair with k-weighting?
Have I overlooked anything else here?
p.s. for this code example, the filter bass drum (top play~) should sound like the unfiltered snare (bottom play~).
----------begin_max5_patcher----------
10135.3oc68s0jiajbtOOyuBbX3G1iO8PW2ubdxq7ZKGgkj2vRNT3XWGc.Rh
tGnAMACPv4h1v529otQPPR.xB.E.YqyzZTOXv0LyJyrxJqp9x+1aeyrE4eNY
6rn+uQ+kn27l+1aeyaLmReh2392uY1KwedYV7VysMawtxx70ydvdo7ckYIkk
eYSh8cLaQ75mmE8e6tb5Jyyju3WdmDr+Y1DWD+RRYRwiIqiWjYdRf6Zq28R5
Z0az7sfGNo86bzY2DWt78oqe9whjkk1uNSfmCdHhC.yITNGo9CBKoBH6gHDQ
eI8ui9u0uf+m29V8udvS1dY9KujrtbOOTl7Yy2bFb14rpfOye1YOm+T95xso
+pQZHmCt.ShnZNgAwyoODA02aDjGX1BzDaIlB1RfFQ1B0DaQGS1RZYKtfbtJ
4T11wl.lTPwSFS9Wmkkua05jsa+qyhT2zlj0aiKSVs+FyRWmrLe2Zyci1S5E
IaUur3xz70O13cTWjg6gHqAgCUZj.BfbtrlvgCvpShzWBiCrv4o3ceN5Cu6S
IoO+9RE0D8TZlxeaz12GqbTeIITc9uxXYwtEN2zvfHQfPNZNS8ChxwBj.hnT
sqYvbJ3vOPHQo2.MtswgV84O7TdQzpzsaxh+RT95ru7+tIiFPXz.DJyCiOMn
lWjbSGQfaAGwkggiHRP33n0IeRQamwPahVmW7Rbl1ATaQazXjF7tz86Ehlf.
EFWWVlja9MBoYx5OSRgi0b7lxsYZVxGSJ1pbxT6K7lYwa1T6zuo1inEH+Rt4
EIdn5ToqsmBVcphjOlt+4oUmMtPQ4kJxdWgQtL6yLxrCul7UIEq2kZdS1SpZ
ZbjjoQXsJZrsahWZeXca09KWSE1XFBQFWYLkkp5uHBvAggpQ94r7keHYUMUG
UKlxub5559cO5xqRTtpxJerdOMPz7Fu9SNJrwKp4AC4+GKRiypXfmKRWkuVS
DG0RnO89OmxcjoyK8uOvLl6Xc7lFdXkJlRrzxE2pXxcaWDWnanbNMQ6uXYdd
1wWp54xRdpzc4MoqWehTrLeS6WrP6ju8KuHWcwWtz61bksOtas8pOpzIJeba
7GOVZWFmk4rTO90+430oun55sL01Df.UWzFe+62trHOK6H90dkO1vUVozwWl
7ozUku27gpqLnt8zM6UhlU0JuJ84jskGetx3m2d7Y1V9EqPu1o1svYC+XYxK
JOmkmbCJqizskaee9m15tw8JZ0E.GF.Uca55t8N57Wx82wt.WsnLOt9UZ2A3
oNAw0erl7C1tuvV8GZbGhDFyEr7f6v8OkwuuyAS3EFwk4qVzOgAL7BCpIxMN
ZDkEJuxaieNoQgAbdz6XygHFGE8NU6BjSXQuSEqMQEUEjG8N5bLVcBvbDGqu
G8kfBAUD8NDbNmyvD0cAYykLHBodVDdNlBnX8qgqNDBE5GSEQOAYtA0gXDkv
jp6kLGphLip+Bn4bARxnlWFFKvbo4qodsPFQcu74pGGXtWwbUPdby8pNTphB
1dDmAEpCUQPf4P.GZdAbFWEfn5P0GCI3P6KPhz2sgIjDIjyMmkvgL.yPBbAE
vM7f.RwBK0R3BH.ZXRflg4tWKEPHluKAAIPyIo.HPpOoJlMIlSsRIhjSEXq7
foDnbCmSoBJUcup1eLFqERJor5URH0azNJPatnWZvnV0fQ8UCVE7sM7Fl9un
lLm.AH9zYQ++5cQv4Wzh9or73x1MqggWpnTSriW05rSpCycJ8xotuzW18hpe
OODLODMKc8EjO3dHeP9IevFsFNYp6EnLJKJ6x8B7vk5IfzitBthHgBrlNfai
FyGS97lhn+tmfQ+eT+FE8OtcYbVbgNt+HXG5ur8vnOUFJGnYWKQ6eQwKB6xi
DaTz3LrP+Btf0tJEXXQWfAyk5e3bfJnZgDwLmydEvQzy9rBTO5UCctdUxmqM
zufHrr7QKZGLZOrv7RE.irxCAxIOvAVdbX3e5traIndC4oudyBps46JVtWmY
u5QzwDmZfLkoqqFM7eoJH0HeUp6JQf8jFzMdiFQn8a3EUbN0lWrxlmE3skxT
ggEAalx.iCk4s1ibLa4Hmw2sPE3wjJ7UTPFSh.1kFD3XQE9ZPCa2qh6j6SF3
LcFeV8nM6VOFWVVjtXWo0KX8ra1orv7bV9h3rSRcRSIo4sGHtac1iYgI6wbh
7qYO9qYO9qYO9qYO9qYO9qYO9tJ6wuS4tR.EXTz6vv4DhZjTD0g34PFEHYlT
pBYRLPcVn5FLm..UC4hXRMKjPETc1gUuFBkneXHdNiKQ.S1P0KtAFVeDFxX5
r7xlKnRlfG8N9bt.hDPSxoEbfPmVU9bHlPgBy6A.XBf4NopNIDpSRlivLDT+
ZjTnjgzuZtZbwH6qgvwb86lLmQnlSpHLJhSs4WlXSQKERMYgVoARfPyiRmKU
Ghk1CYBF27l4bhhVzuWFV8H5jsiUeYA0jybEWw3HgMM2JQG.gshIABAvlTSK
3Rl9cAmiDHpgYU7slGTOElOWxY.2YQZxD1d9hYeMeweMeweMeweMeweMeweM
eweMew+tOewgH0N+tIMW2EY769H4m2GIB99MQ42sStvcwbuDfYg52I4KtKaj
G1ntqITiBVb9xfmpiK7rkA+zsSQ3va.OyjSFO2zV.hMpaAHHE51lGzaZKKCN
EbIAPBNW9xtrxzsYoZ+zsNYNOzxD5P48diGtU8u2m22lES622L6EQhCOo58o
XBK0YGRxoS9SyadQIroMuHvtwFC6VrnLZQzSWdqb9voIU4HQaWraPWcCxz79
17jAHGFN+vff+GZcPvdNggzl6j.02MuJQ1vlnylp3PKE90rns6do6lTDZGX4
q2tynh4RHkPoDBQo+SgRkeD7XvwGZ2+60s6cqkFACSK8d1Vu5qOskVvFDaOL
Okn6DOkvK6oDBHrlBbhcdGO2oNNIhv33DBEx4vSkDM1E7cuezpEM+.stZV6f
nmvhyBK4NysJLLtUaVq.yZPBLNdYqOyyd15CCypto4FejnAWCmNuqc0S6Qyu
Z84VELW4ESOogn4Q34QD2e5l7.OlFCH8jwelw.Be6554URL5PD2l+XBN780z
lFk58Q3PISQgHrPOO3f4XHPuMuTwKCjHDReIj4ehXDf9FfTjdJ5UOKFJODhZ
ia5e+zHkgQiDuGiVPGElKUHqjfXZfGM71WxyKeexpn30qhVk+o0aieYS1U.K
h5Zmzvrs40I+PuB3vhi3cKTPHGEnfnHYqxtLdcYzecV55OlTTlr5uNKZ6FEQ
UbnSpqJAHgQBvUddz8FqFjir1OBgdPNP9XIBRJcPfg27KJPs3X6hlfyMrMbP
LXaNH1VFWTpWKFx4HNAyYZQ4gioft00CiGFKcoYx9ITzbH.PEDmxNEowJB3n
z4qURn79IfDfg0qcXGkBh.MrdtMqXv4rSkBPNcPRgjecU7xeqoL80Ee0fqQ6
TJ77VPB013FXL+HK9K+Vzuju94rjss1dsM8405UavEPaLNHLCvx05IkmKA3C
K9w1A1nsqiKRT9n+CJk4mSJaBGWpVCAypu1lQAwkkzsvTL4nv1qTvAqFa+uQ
+A67T0HGhGONjxvG3PIcT3PiN7WlGm9TTrpyGcPsQhF3ypk92Q7YXvYIWnVN
zGBAlLFUMXaYSymFQNdLK2hTTNlkLLHIZh5okDpdZMowPXBs5UPWqDVH6ZEa
2.FCruz1XanYj7m8mNxvf.MZd27nYsqgvQI6UahdIIS0w5pq1Abi4sHngMgP
hut6oNZ2SAAPWVFnec6S80sO0W29TCa6ScbTMmrkg1sJMOR4tZVm2NA8dkqJ
wmmWDpMS0TwwgzDnEm6kj.JEjsa+snmiSWGkoZKhRW2hrPFdQAlxlS3bIfPj
.LWCFTVf.8g8apfIUVX0FZU.vCu.PPOWWvx+zwg8uvlFX25eIWoDvu9Nons+
uskCOE0CIm3JpN1oxvlsU8f2m3sXwe+uckcRwIAP0ZPTAbiJwYv4RNgI4.ks
jDPAbkrggrXI9TusbFpDhfCuDhoDF2ORHmuWljQlywBpzK40CWWxwB+l7pYI
mdKOBIHA09aFyjiewqMUMDH7pZTUeaLLChYBhjA3BJrEA1qOSSDM7xKBELGI
4TtFcKoHJTZhE.O+fzhCwX3MzPU0NphcSuIikgwPEIBugZi5cMJGgHMBhpTB
ApwfCDHFk8JqOzQXy9hUAdcdHoH8Fhul76VpEhIBhhZv.LILZgXT30Ba1ZtA
wHDQuQxQDVnwRW4wNy5uXjNBas5F0FQp1+CxP0uw3Wk85dgMdc+Qv.BcNDKw
DBhgPRkGPYKBrWe85RGA4EjvligRFGAwPHgqDNtxzQ8vTnzan+NHkqcav4v.
4uiJCugZy5cMIGuAN7Fb3diPzd74jyVbPR1bTc6Tt3Fp1I4h4PMlhGntGXiA
xazj0aihQnArzObmTB7lHUo5o3fyor.YKC4iPrKMoaZgegwpW1qi0DWQNHXg
GwIZRNXw3k6ADmX.vygfGdgkKejCS9flJD4PHBetraRcghEgVeYTPjCsFgW6
cdcpriNkKxrSjra8ke3Wv4i0d8Wat62d8meY50zToKMGX.hiIO3NEVBDDf5j
ly.HPcwu.PQHkqa9XxX5dI8BINniIFXv7EPGniIpjPk9JKviMUbyQnEpufag
1y13QE9pchQiMU3ENnLlvGDE4q144fqysvkogdYdPuD78C8x8oUVb+PuXe0J
uSnWhO3bD89gdo9Puf6G5se3H0MibQ91M2smdI9FAHYLCNvPEPecRMZTA9dH
3f8r3MlJ7saYznSE.ectNZTA7dnEAI7rEYuI83QE.e69XznB5cQKB3tfJtGH
BS9A7Q4jgGapv2XEt4vu4EZPNjbJypgtkrScXwzqWvo+nYIs+32mrd2gjfse
w22Lsu34mRyxpB63MmcGuY197f5BN4gZW5nvUPZzwW7fAuAvbMbBqNRcfYpp
pKLbOGb+CRnDI.oucBCwITyQBDlhMw9zvihN7MAPo8KAjBaNlv5SAOBWfbKQ
b8FE0jbTNnNtPqZfKx2jWTsmGlikG8b6JyetHdUpKCiUXR5g1qC6TCKpTnty
yWD657ppg8h5uilT2pZT+tcKi8sg7nlBBmBwF4HRhER6QTHPOUhmHVlEuboh
ZO5w0UtWoQTRnJwp4Ht8bm9z02QGJk5+8MIqi9w30ai9wjWRWjms53Tmmjk7
xoeMtfw3FRT.zEcXyQpOLBc9maq5ErT2Nc7a.o3LCYBYbjUqQ..FbJ4jWfdV
jLO6iF7MXaRklDVhfLqfZu5HhKH3y0jTFMGm4S.AxMxKknlv4VFPulUzGQYm
7r9avUozcAatNn+erUmnxVSvATgvdTiL7oVcr8ZEZrhgwsGYeau9M5993xRe
M5puYm9Kmz4W8MJkFZcNd7ai.g+m+ikOZdMfd4yPR0NvsZrDNvnTo0ov94yv
echS8YX2GXGOL3rj3hZudncXvRkwE09QT5rbbGLuOerzWxd1Z.0zQm+nu9Mm
6ziNF1ysa0fFcqle9m9W5k4BTGii0Au1FwzeAeezNW2bgB3L6LhwnXnwbQWk
gPWuK1+0urpH+4j0+jQs5ZctRXPHvFQkDwHFcKpDJLqjiS9PUg4drNoNZNSe
pJ5ixrwEnUSLrr7RFRPFV4Jw7n506uzcDPdGaG4erO2cwh1tYjXzMiLqVfzk
8KZUWuLMcjGlRc4wOwV5aSVm7w3YAnKjlsc5RuNBrjac8hktNh0mhhGlwRKC
ZC18O6fz2OkUcwZe9QCxRwGiA4TYK7M6JKyW2CKBWzNhJ4KvcDbpH8+zQ0mo
WQD92Fmt925kSHbUu3mezzQ9a+TpxOhuLvYNCgN+LG90jR2nWcD9+1QPPZm0
0OghuVrXcniplSzQWdCmz8xklLwwS99cUvlYO7izVGmMIaY2D166iKKR+7xx
hr.wkSBQqALWucRNTE4STCuKby9C4qp.Lvt0KQGhbYvRtaTXK+PucIdqbx7C
6dYg+DbSdVOOvkIj7+yoKK6lLuWZVSBqXPO2WkQN9iKy2jzuPGOLqURr9G+F
u2cQC1OEuXzGxdSZqW0O5jv7pQ5uXPCRq83+ZHOE2Fmi+T9y5wOOJCI5JMxX
Nivg1mhfglDDPbSo6Tv5+muzgIB+NXvH+b7GSdJu3keazas59nK.yoirPXUb
wGd2ZMB48NSxz58XI61TYUktudLaHsj0ORkKMd0LIWMmxBCcLB49FdEytQKa
diVdumpY78Wb.FH.TauMOFudTWlW45yP5hrDUuT1EVw2jm+gKOaoWbRL.doB
eX1bO6fwKUz9S0utTduvX5Famp+xlz0enWcmvTx.fnJjErF+eH9sR.76IaLK
N98nm4y1ym6bCkCyhq4Qv0OxuNM87S2lY1CG86qMEQcnqo.tv97iEuAcC8pa
sE8A637+YMJP+ZHvzLc3XcaHRMZVWE8Csxe9d0iqkuPfj3V+hRIVvcGwESxn
jeI9yrZvrcOBEUb7Xb4Nk5QXcKchxw3GvtV3bBzIzkLHfvTj73930d2fSU65
wX3+UI991BEzP6EUqstyO5JNV4B8Jp9gFO5FEhTHcIetkZ20HNEmK5ZhuqsN
1mr73YwImuIaWx6fCvMEFxcqTqC9pk08POELQQ9mVOHt3p8yLAbw+zWhGFS.
PRpcc5w4XLxZiifpHUmNl3aKRRFHWXZEpRGNjoicc5XfuW4YecY7fXAAAvX1
j4y.JFvzjvjF7mbp3i+ijUChG3UgdCqFSMv0y6TwC+WIYY4eZXMEHpcMxxEP
gYLE.pxJgdsIMUu9goR.PLkLJ52yLpYpV+17rApVVkVVpJxXpcIBWOjhQkI1
rqXS1vC7iWs4.HPJSXmCKsaNpGipg.rA+hn.lzXfpwvajXJ3+hjkIoez+U.Q
S5oU4e3.uCpucOFWFvNLZsZX+xsEQ4XW55Xk61vVJqLI9psb2VM2sIGJzVup
5U9PCl+9MNYO4vg.tcN1ILfzsG63P+1tE21lsx3M8Ly+eWbYdz2oyByrQmF2
Vl7ztrrx9Ogw5M.L2HkYUiYDZPN9qZWAETJzNUYLLGa2HlLkKE1zz.YY9Ih2
CbNxPBtvFnJtxzFijX4jzaRotfd8Zb+R9IcVX+ROML+SoEkeI5e947YdLGA.
spgIiKXmFgxijaNp8NSfcXCV17jM.kRfcTLJyJhaYVw..L77Mx0wMFZnHMDM
Ft2w9WvLckqa0i1pz2iwkkEoK1UZg5fZR+tUM4dNKeQb1Ik.tlJ1bu8PxkBU
kzFyBYkzFI.6qZ12w0NaLMj0NaHw.NxCrZY2BOuX2SOkTTw0QGJFwsJ.dJKO
t7x7OIL7uJL5Z0vTHlOFRfxnEQYsxrFd7gVpJsHVX3SWkWFiHl5r1IUastVG
d09XNZsy1RclqINBVU7YUdwTNJJSJdzVrKqadpr.xUTeV5xOb0xO81jCtBur
fYuuUB3vipdgJlqVn5vSqfsmTdd.XsvinjdTaEBPa4vBqFyGS97lhn+tmPQ+
CpeCi9G2tLNKtPWqZqpD.dVWigApPN6JT4XtQCBy.2PUHvqaUHNw5nEqjd09
ApSY3PUnFjfk85VtRbf6+nHWao1iCzeJFAFYN.BX1C.Bt8.hPZNPcE2kHRg6
.r6dXX68.DH68hgL2ATp8.t6gfLn8gfPL1cIBx8zB2SwXVxAQvtWHm6nBz9O
AzcyH2sfTidxQVbh6iKczGG.2Snn8Gr+0YoOkj29PD0O12GE5dHBxw3X4dQA
c+YbeSLwwU.Jj3DfT2IHUQ5XCsdmclJEcq3tGFeftdQold.P1pYODdSLUEja
uspn+lptdSXJgmjx4H0ePXIUnWuFiTepqVTlG2s9Nw7ND80066jxjyUi7iJH
VtUMXTUOoCKn6K3Wh.nHiWCHWXcPAIXp0pDu+LRp0ECT4fR3tDy4RP5rkoPD
04PwY4Rr1sbly9myct4Pt6Tfj1ODk5bIh4bmmKJG47UfrtQHpwm6NiyrGSbt
vvb6eygNePDv9uzd2cDLv9ho6ecLhibUeJmyHjb+qg39.NW1LAv4KS3b2QIN
JlybtrETfUNh3Lt8.DFG.2RUUm7vDaVf7K01XWi19Rdd46+S4eZ813W1jk7i
aTTPwtW5lQkHr1THVCE6m5ijs9qHo3zrb7TZVhNgOtrb.qJr8a1T6zGkVJkz
5Wr42opDWOSwI1SUU8UlUj7wz8OOs5rwEK0I.aY4tBaNR9bsJozLc.9Eq2kV
q1oTk2G69UQmaksabIyaVs0dyrZhFSuTHBwVG1YFgAiyqkupYKdNKe4GRVUu
tvLKeSx5z0azamv0kUnlY0kcYp6w5ooROEnMc884arwKd.+LKpA4EydtHcU9
ZMQbTSg9z0RQoU6lVmYL2w53MM7v1zb0xE2ZPtyEwE5VJWWmnpbVkmmc7kpd
trjmJcWdS550mHEKy2z9EKzypP6WdQt5hubo2s4Jaeb2Z6UeToTT9nNkdGee
wYYN63ie8eNdc5KwkIko1l.Dn5h1vGd+1kE4YYGwu1q7wFtxJkR9xjOktp78
10WVs16Nj9vC4G7H3W8jSsagyH9wxDk+GEWb7Mn2NWaK2997Os8jLQVW.zFn
t5WUY57f17Hvsy76eToj6BAvcgf3Z0EZaAy0d.cMETmOA1053vnFWy5xba8f
6n5UOLl5x3Hb5Jcc0i76JcTcVKEoG0YKnehGk+YxYhG4TWsDiKyWsnmBGzHH
bLKiZtspiMNBifXBeGaAS.AyD10NLV1rAok33Jm3cVSAIXMEHUawqcuoB5n4
MEgESl2z8k8vFkNUiNJpLORD8jVcbazhuDoBQqH9YEwGoGvwWhnQ56UeWGUa
eOZ3j3lkixvW7G0EFU8RninK9rLjfKoXNFQ4FrgvVaLI7ITPt784ahxe5onW
RKJTlrqbhxtJq3gWVI4VQEDNGBAX.lgjBFfqWeTLvjKonuaSd55R2vyS0ylX
KhHTKU13wPchLWuCOwXz4ds3lYaFimPYjUIJRw.IEWSQpEoDM7RID0JkPDS+
rbxjKWVlqWtKkZuPGGEXCIOOfLtfZ3aA4PPFHvz0E1KIwquXOXUK.gTsJQag
+1C4xUpb0bfypQbOLzfeMK54h7cahDCXntvQnroy4FwDkBmiwRHiSjP.UXVD
dSe8lOPZS8ZnldJn.pN2q0ot.eiTmR0teoCQahNZZSDFaNTvnRnR9Pk1MAFg
eCjREIeb.hHDL7hHjRBnC4AA0k8EgfgELHTx45MQA9VHiTiZbYRDlMDAEJ7B
Jn.XDTPlXNjpBelJAbBiB0a2go20zunBLLB22r6ztmabeGslqCNjZPaX.ERg
BHQhAD8hPGxgGulhFe4iYk4Y9ueMy.SIWTTUsR8p8+6et1kh8wsN0mjjAQz4
zZt0Y58vFBPcqGc2O5Ux9qK+WigKdmZ2cl6KxPDSrQSL0nyKJ8UoXBOBgepL
+LALfvyYmN9+ahXxDk9PDRjQSHgEJeUXB.RYbld4mo2OXT3sPWprHI9kAE8I
lOdtljz4BUmgXImIXJEJN5g86HgPKmNA9X5TPAsKA.CXJeP198sqfC.ggXbr
t19gMYSCeJ72sOiFGu2WTD55UIet1ZmHHRqSwmjlWM6AL4Htwiv..yna4NAB
AACq.4v5mPm9qVlU7tVDVEdWffY2C0i1yK734EqrqRHvskxfn1IM3ss94BG0
RIL1aIznREdWLgoStJD1+FJ7jqDY9j9TPpM4xY7Z.QLuMzFW5f5McLplU5wg
FQ7RogO5zgeJujQmN7ROEwFc5.4s9AbToCrWzwnVD2QXu0OFW8Tj25GiZGQ6
e6dpefFM5vaxXTMagd6NENtzg2twF2nkfdatHl7PA7m1HSdLTAnSnCiexr5v
ZY.TGVq66Vkl+ilUb9ieeGJQFADRo0XeAzhv6ZD31htn6qdxWBUoqgwlUfgM
Qiho3vBR7u5fV5ua2x39ADubJD6PXYrvg0xT8l0vKjUx+5k7oPnx+9lDWIM3
GSdIcgFLutJJ4vELF2h.5.nPXOR8gQdWjS3HEmIrneEGY0ZD..rKfxLpBOmO
TWOPshC6mfiUDH2hdURJwA8XDjzxTT1u6Jt79CaMuBM5993xWmXeze9OV9n4
0.5GXW0gBrSi3zq2PYzoUBEy1z5hE0AG5mKUFWT6GQoyxwiBlqqsm2CBjmez
caMte.lyc5Qm1hbOZzsZ94e5eoWlKGpxHzpRyEeezNW2bgB3LacSiQwV3gEp
FMF55cw9u9kUE4Omr9mLpUWs3jxfPfMhJIhQbvkHTzDD10LDigzQyYgVRDjx
rwEnUSPmCwXmB.fLrCAxgbBSJcGAj2w1Q9G6ycWrnsaFIlpxc2nW3IavTpq0
e2Z1Reax5jOFOK.cgzrsSW50Qfk78UVDWGw5SQwiRc.B18Oa3JPWcnhKOFEn
qIxV3aFTYH8lV3b+S0137upH7uMNc8HUpMmDxe6mRGRYx7VUkSczM5UGg+u0
6Bi9UpUvCsPw28p45U5d41Toh+tjU82ORacb1HTKeSXuuOtrH8yKKKxBDWNI
DsdCL+aiZco+BUIg6A2r+P9J+qTB8MxkAK4tQgs7C81k3sxIyOXJfI9RvM4Y
87.WlPx+Omtrrax7doYMIrhFbmJeUF43OtLeSR+Bc7vrVIqvp+qOdu6hFreJ
dwnOj8lzVupezIg4UizewfFjV6w+0VgZYxcN9S8u7Wb09puRibKUKXvTw5+m
uzgIB+NXvH+b7GSdJu3keazas59nKF+RO6p3hO7t0Z.r6cljoMfRhTWlJqyp
63cofb2bV+HGJMvUyjb0bJKLzwXVPYmfhz8zTKYmpY78Wb34G.TuNVMBudTO
KLM+wEYIpdorKrhuIO+CWd1Ru3jX.7rH1ue1bO6fwKUz9S0utTduvX5Famp+
xlz0ene0SOcgtRTExBVWiiH9sR.76IaLKN98nm4y1ym6bCkCyhq4Qv0OxuNM
87S2lY1CG86qMEQcnqo.tv97iEuAcC8pasE8A637+YMHM+ZHvzLc3XcaHRAt
N3ozBHt0unThEb2QbwjLJ4yq.8ctnpd7Xb4Nk5QXcKchxw3GvtV3bxl8sKYP
vUwpq2Gu16FbpZWOt1F7ldWxfuRKTPCsWTs15N+nq3XkKzqn5GZ7naTHRgzk
74VpcWi3z8hcWS7cs0w9jkGOKpD7MY6RFTw6FC4tUp0Ae0x5dnmBlnH+SqGD
Wb09Yl.t3e5KwCiI.HI0tN83bKLgYJo0pHUmNl3aKRRFHWbqpJ0VF36Ud1WW
FOHVPP.LaI3Ev.PaUVkyjPIc53i+ijUChG3UgdCqFSMv0y6TwC+WIYY4eZXM
EHpcMxxEPgYLE.pxJgdsIMUu9goR.PLkLJ52yLpYpV6VMe+tqzsuYWwlrgG3
GuZyAPfTlvNGVZ2bTOFUCAXC9EQALow.EInLzjTcuKRVlj9Q+WADMomVk+gC
7Nn918XbY.6vn0pg8K2VDkicoqiUtaCaorxj3q1xca0b2lrd01Wi8JenAye+
Fmrmb3P.2NG6DFP51icbnea2haayVY7ldl4+uKtLO56zYgY1nSiaKSdZWVVY
+mvX8F.lajxrpwLpycXSa1jS2pHBJEZmpLFlisaDSlxkBaZZfrL+Dw6ANGYH
AWXCTEWYZiQRrbR5MoTWusdMteI+jNKreomFl+ozhxuD8O+b9LOli.fV0vjw
ErSiPiiu14n16LA1gMXYyS1.TJA1QwnLqHtkYESWmbOeibcbiAlElFC26X+K
Xltvxs5QaQz6w3xxhzE6JsPcPMoe2J1aOmkuHN6jJzVS0Bt2dH4RcrDVtIdc
x9E7q5V0XIww1iOT6W0KUsKpvcBz4UtRIsCktRP6ktRjsn8vLP4GzVFKkrZT
gtLPV+czTJ6NyEyCG8qZE9xSxpG89QdRBi7DaqvkVAJyBY6TB++OTfhCi.EB
vzVqj5JmbFEWN3VHfM2zw.VoUdeJBv3j5mg7KRPcneoEXegVCxuNqk02uDk4
wWBKpCyTydIckoX93XNlDogDct.ddYx1pmegKgbkJUjv.q50KYpm.8O8lE4b
OXwPHKgPO9PmPMGCgP8mG8oYDBB.SR7gGYiAO5yWF0xWFN9MrvQ4Si4cvSPX
+zd4ZfNJpyDpOeZZH7+QmLOszibhdguDbfeIjOpqjPH87R67DxITpHDe+zvf
aS5i2fPzehOtZGCYqW5OvQwSqOeYRyeYzvzm75SKBQOnBObDPHAvQ.QzAw43
aMRQiRnO9DqLSNFZq9+ogglqY9zzxCQ.eL9T8kH97kvgneKBax9RfNL9pg0q
jOZD3wIHUu+zA2N.S8U9NzVRDqCCBX3eInOeogpy.8gmDiRG8dIMEiQGFdEz
pnkfLvC5S6kcBepBLukNlPmkIq3Mazygf6oMezYuD+K1rjIdv7OSWa+ml73M
qH4io6ueSchaVbwR8DkrrbWgMW5elYyrpIsbEq2k5TpLo0+DzJ1x7WAkhOYh
W9ausskN69IDn4MtPePi3dhDw8bSKz7pis8UFaKqJ18SZwCus8of43oeotlX
CnKbyM.8AQg6OZB2AjDdHnH7fPP3Aidv8E4f8xX3z0Od+VE28DVQ6GBAeeYP
b.4ea1fnkYut0YtdvDzoH5qG1odt0m6OB9dYz6sWH2a22aE8Dwde0YF48iEJ
6nl0nQASitBsc8PU1SD1s+nqqWHq6PPU2ggnt8CMcuc53dhbt25XmZVEWDLU
7iPBWehrxOnzY.He6UP81d39sanca+P519N.fthrs8UerW3Bm2ZwWRYUFZc0
5HU6U0XuNTcEJx5.JzdGQT0PXVOLt8BtCCFoUG8Xal37F3UCLMgtqHpiP8U+
zsZDouFBDONLDd0OzcMTxqJTb0W6vl5DveTaMTj8onyZun9fRP0Pd0lIlgnP
0GjVMTbVMDU0Cuhd1a4fjFibWl+PmbgL1Fn0Q.0lIlNi5oghzNEcSCndePIy
ZHW5cTzF0QkTeFKwUQhzdgBoghapPaz.NrnditnAioNAEQGR7DdiZnAi3qsg
mBQ3rWnQ4ZnAZnXoZn9YuZJBIsbBhdFPI7.PvyAybMiTmdFau+ontuHy4vQk
yAjCst.+YAIyCAO+YgbFUNCYMCwqBcs4nwKjyr2nl4.PLyAmRKOQHy6ZEqVh
OOTNmpg3kd3t85PaX+P3xdhtk8AYK6OpV1aDsr6nYYOQxxgtHP7.4JmN212U
y084HQ4sKXoyPYR+Ginm6Z9dgpjCluNBS57N7nqiXjCc9xaCoHCBCWCQH8YT
ddfBjAgrNBsGalv5iTcvgI5KhN1Szbbj6ReHtpN15vuVw5HznuIc6Bnx3f0r
NG8E81L2KDWLTDXcjUzaJzKzTLPTXcTSzaBzKjRLPD3QHhn+T3Uvao.Qbmf1
g92UiOHbXfnwZHYn2zmWnWXfnuiQoP+Eg9.XeWFr9BKCfdMx.mgpf9qh3Cvd
MXBrNhA1wfG7Dk.6EBANX95Xj.zecFeP+ugSbmhxe9Ldd+P1udgpeClgpgde
2O8fbNx74ypL1Oz361YvVg3ddkkvyPYu.78a.M87Qv5GJx0KzyKXL0HwSAb7
8dgHdCWdTg7c2I6Wf5HZmWJ9mihcCCA6FJ50MLjqqUTqqaBV6VmyLCdZQ01M
tlPCna81+m29+CGo4bbB
-----------end_max5_patcher-----------