Well color me interested.
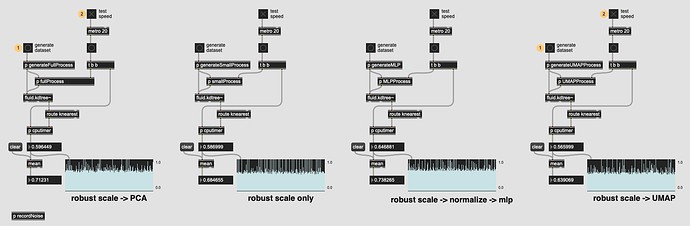
Based on @weefuzzy’s comments in the LTE thread, I benchmarked UMAP vs PCA and the results are really impressive:
And from my understanding, UMAP is “better” than PCA in just about every way (particularly with lumpy(/musical) data)(?).
It definitely takes a bit longer to do the initial fittransform, but I’m not bothered by that at all since you only really need to do that once (and it’s nowhere near as long as MLP).
Archive.zip (151.0 KB)