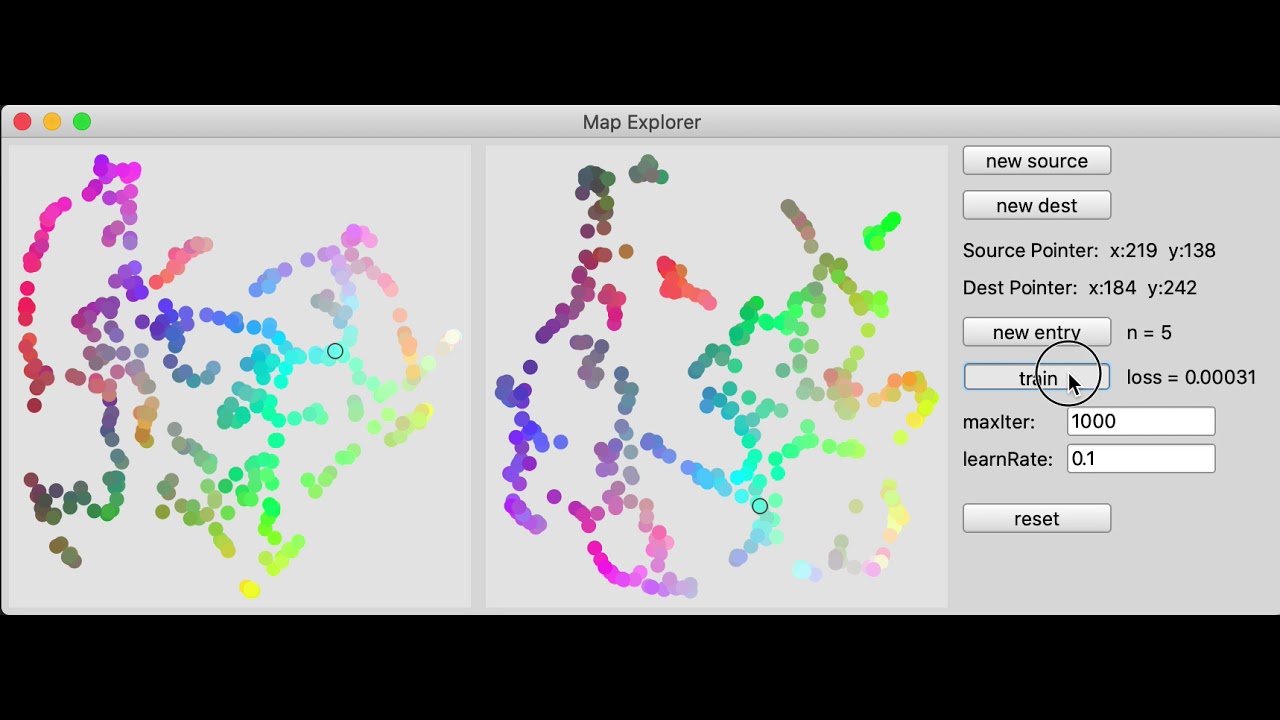
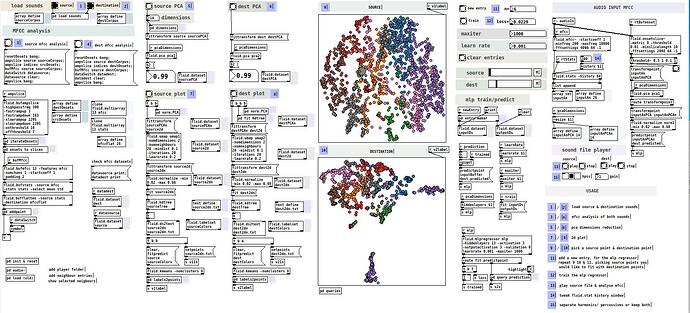
Dear all
As explained in this post I want to map 2 bespoke, non-overlapping timbral spaces that I would have downscale into a latent space that made sense, one for the source, one for the destination. I had the idea that MLP could help but before doing fun audio that distracts me and composing for real with whatever I hear which might be right or wrong, I wanted to do a proof of concept of mapping arbitrary 2d to 2d spaces via dirty, low-entry-count, assisted learning. It kind of works and it is promising. Here I share the test code (in SC - I’m sure it can be improved by real SC bufs) and a little video tutorial (for those who are curious about the result and also as a user manual for my code ![]() )
)
Feedback welcome (although as usual I release that before going offline for 2 weeks later today, well done me!)
(
var w,v1,v2,sx = 0, sy = 0, dx = 0, dy = 0;
var tdst, tsrc, loss, nbentry = 0, nbentrym, trained = false, maxIter, learnRate, reset;
var source = FluidDataSet(s);
var source2d = FluidDataSet(s);
var source2dN = FluidDataSet(s);
var source2dNdict = Dictionary.new;
var sourcecolour = Dictionary.new;
var dest = FluidDataSet(s);
var dest2d = FluidDataSet(s);
var dest2dN = FluidDataSet(s);
var dest2dNdict = Dictionary.new;
var destcolour = Dictionary.new;
var umap = FluidUMAP(s, numNeighbours:5, minDist:0.2, iterations:50, learnRate:0.2);
var norm = FluidNormalize(s).min_(0.02).max_(0.98);
var inputDS = FluidDataSet(s);
var outputDS = FluidDataSet(s);
var inputBuf = Buffer.alloc(s,2);
var outputBuf = Buffer.alloc(s,2);
var mlp = FluidMLPRegressor(s, hidden: [3], activation: 3, outputActivation: 3, validation: 0,learnRate: 0.001, maxIter: 1000);
//make a window and a full size view
w = Window.new("Map Explorer", Rect(50,Window.screenBounds.height - 400, 860, 320)).front;
v1 = View.new(w,Rect(5,5, 310, 310)).acceptsMouse_(true).background_(Color.new(1,1,1,0.3)).mouseDownAction_{|view, x, y|
sx=x;
sy=y;
tsrc.string = "Source Pointer: x:" ++ sx.asString ++ " y:" ++ sy.asString;
inputBuf.setn(0, [x,y]/300);
if (trained) {
mlp.predictPoint(inputBuf, outputBuf, action: {
outputBuf.getn(0,2,action: {|x|
dx = (x[0] * 300).asInteger.min(300).max(0);
dy = (x[1] * 300).asInteger.min(300).max(0);
defer{
tdst.string = "Dest Pointer: x:" ++ dx.asString ++ " y:" ++ dy.asString;
w.refresh;
}
});
});
};
w.refresh;
};
v2 = View.new(w,Rect(325, 5, 310, 310)).acceptsMouse_(true).background_(Color.new(1,1,1,0.3)).mouseDownAction_{|view, x, y|
dx=x;
dy=y;
tdst.string = "Dest Pointer: x:" ++ dx.asString ++ " y:" ++ dy.asString;
outputBuf.setn(0, [x,y]/300);
w.refresh;
};
Button(w,Rect(645,5,100,20)).string_("new source").action_{
sourcecolour = Dictionary.newFrom(400.collect{|i|[("entry"++i).asSymbol, 3.collect{1.0.rand}]}.flatten(1));
source.load(Dictionary.newFrom([\cols, 3, \data, sourcecolour]), action: {
umap.fitTransform(source, source2d, action: {
norm.fitTransform(source2d, source2dN, action: {
source2dN.dump{|x|
defer{
source2dNdict = x["data"];
reset.doAction;
w.refresh;
};
}
});
});
});
};
Button(w,Rect(645,35,100,20)).string_("new dest").action_{
destcolour = Dictionary.newFrom(400.collect{|i|[("entry"++i).asSymbol, 3.collect{1.0.rand}]}.flatten(1));
dest.load(Dictionary.newFrom([\cols, 3, \data, destcolour]), action: {
umap.fitTransform(dest, dest2d, action: {
norm.fitTransform(dest2d, dest2dN, action: {
dest2dN.dump{|x|
defer{
dest2dNdict = x["data"];
reset.doAction;
w.refresh;
};
}
});
});
});
};
// monitor pointers
tsrc = StaticText(w,Rect(645,65,210,20)).string_("Source Pointer: ");
tdst = StaticText(w,Rect(645,90,210,20)).string_("Dest Pointer: ");
// entry button and counter
Button(w,Rect(645,120,100,20)).string_("new entry").action_{
inputDS.addPoint(nbentry.asString, inputBuf);
outputDS.addPoint(nbentry.asString, outputBuf);
nbentry = nbentry + 1;
nbentrym.string = "n = " ++ nbentry;
};
nbentrym = StaticText(w,Rect(755,120,210,20)).string_("n = " ++ nbentry);
// training button and reporter
Button(w,Rect(645,150,100,20)).string_("train").action_{
mlp.fit(inputDS, outputDS, action: {|x|
defer{
loss.string = "loss = " ++ x.round(0.00001).asString;
};
trained = true;
});
};
loss = StaticText(w,Rect(755,150,210,20)).string_("loss = ");
// mlp parameters
StaticText(w,Rect(645,180,100,20)).string_("maxIter:");
maxIter = TextField(w, Rect(715,180,100,20)).value_(1000).action_{|x|
mlp.maxIter = maxIter.value.asFloat;
};
StaticText(w,Rect(645,205,100,20)).string_("learnRate:");
learnRate = TextField(w, Rect(715,205,100,20)).value_(0.001).action_{|x|
mlp.learnRate = learnRate.value.asFloat;
};
// reset
reset = Button(w,Rect(645,245,100,20)).string_("reset").action_{
nbentry = 0;
nbentrym.string = "n = " ++ nbentry;
trained = false;
loss.string = "loss = ";
inputDS.clear;
outputDS.clear;
mlp.clear;
};
//custom redraw function
w.drawFunc = {
Pen.use {
source2dNdict.keysValuesDo{|key, val|
Pen.fillColor = Color.new(sourcecolour[key.asSymbol][0], sourcecolour[key.asSymbol][1],sourcecolour[key.asSymbol][2]);
Pen.fillOval(Rect((val[0]*300+5), (val[1]*300+5), 10, 10));
};
dest2dNdict.keysValuesDo{|key, val|
Pen.fillColor = Color.new(destcolour[key.asSymbol][0], destcolour[key.asSymbol][1],destcolour[key.asSymbol][2]);
Pen.fillOval(Rect((val[0]*300+325), (val[1]*300+5), 10, 10));
};
Pen.color = Color.black;
Pen.addOval(Rect(sx, sy,10,10));
Pen.perform(\stroke);
Pen.addOval(Rect(dx+320, dy,10,10));
Pen.perform(\stroke);
};
};
)