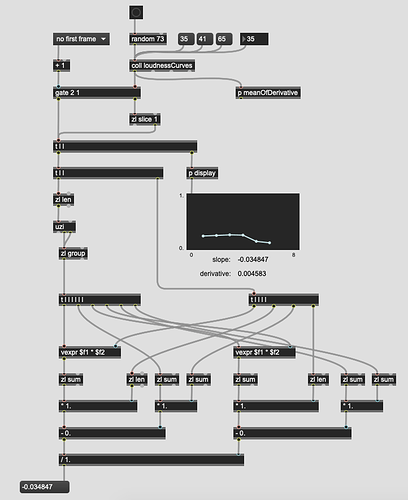
After all the temporal/morphology talk in the AudioGuide thread I decided to revisit this thread and idea, and wanted to figure out the linear regression stuff anyways.
I shall save you the details of me trying to understand how to implement linear regression in Max, but mercifully one of @Angela’s friends is an MIT’d data scientist, and he held my dumbdumb hand through the process…
But here is a Max implementation of the slope output of linear regression (based on a translation of this javascript code):
----------begin_max5_patcher----------
10086.3oc68s1aikbcsetmeELB2Oknou06G4SW63DGfXmDD6KLtv3hFTRr0v
YnHEHo5oaGj7aOqUU6CEoDOjEkN5gM7X2pUedtqcser1ONU8e9ce3rKV70Iq
Naze+n+3nO7g+yu6CenbHdfOH+6Ob1Mi+5kyFupbYmM+tatXxxyNudpaGu9x
eX57q+zxIWtt9Xb93GUmOJo9nOoBZsSi+3C4v4i7JdFi4ipQ++kGvh6VOax5
0e61I069ryNezYWLd90ms4RldU4Eu3he76MV08u4kiuYx5IK+zj4iuXV41Ux
4.MNcNdrEJVe+AqurxQM7f+We22webdiC8KWbyMSlutiBVO4qkg7YWMY4zuL
d8zuL4ueC0sbxJbo3fKl+oYSmO4xE2Mub0l94b1j9i9yG4xwO5R1TLF03Opr
2b9nfsv5Taw51luXRm09XW8DF6ed1B7P1LzWNESQ6xz2mnfKUGPgGOfx5mhr
.44WtX1hk0qnHOc+Oz8wchsH074EKuYbgxCGhWdw06P.ly24G2S.Oe4s4S9Y
P9ORb61Q2LY77+sO+q1H1c1QmBzQ+G8XNHDRN7mnMBpUq8GeN.S7jorW1Z3D
D5zaSiSVJCaYbCl+zYS9xjkqf9xVW8GNa7s2t0g+vV2BYV+XcdHc9lCMcd8P
5MGZ4juLs698aN53kfSsFro6VVFom80f6r6eLKfN876lVdR0ChoMgjJSPygX
zpaGeY8l47X2oum26yEgRkqvkCF9Wtr+dtMElls3xeZxUaIGh4famLe57sMg
ryouZxmGe2r0e5yKlud0z+TgBz7gumy+YgB26I4XnP9+BnNOay.35kSuZwbR
D6LSvC2859iiphN5cFLkqX93a2yMC4EvV54jqvf7tUWLdImnDkRS2IWuXwrc
O0l6a1jOuVN8sSmO+Abw0Kts+Stb50+vAt2KVfSdygd1kyr5S2Mud1OAYh0e
Z03urK2d83YyDs3ce7ec77ovXyj0SqSAF0lSVML8Cqtb4hYy1Y7VOyW1yYtB
x3WN4mmd05en7h1VX.W9za6DhNayr7USudxp06dr0iud0tGY05uUY5acn6tP
zg+z5I2b6LLJ18Bf1wzUqW8CK94UxE1InsMC3dTGaqSusIwcN9gLMtq4QZbb
6SrGihUbHVs8wtkr4GZR7PlEg+ooyu253isPp2lR1mUx9bU7gN2EhsmgmOc2
7ebwziwopdo0oxeIXPNJugrkxe5mundB7E6qCe4OMaz0KWb2sMICYhENiWeB
bld4J5XubEyaszx5QWLZ1n+zrKmMY7xlXMZk7WMxaJ.8DImt2S+rJ+6WAn+l
uG.QOtdkmLkBz.mp9OZylS+7D2SP7Q+poTsZ8xIiuYjoMKN1ziwqFhChVl8M
VKq79ZRExU8Ss4mGYX2u419kLT8KYr0Y5h7ca+7kWx7ql70gVLpRCs4BOVcg
mB45+kL8xu1gg7TLendtLj6QJyLBzC9mxXkme+bpUKta4kcy3aLENxryPEf9
VOc9lHG9iaI4OBLkllqNY5fBYiTMQG9WR5n6o2.cDewoC8a+7R2S+3zAQk8B
JenZddw8hSG5loC8K17h6chbZrY4C8K57htY5ne6GxA6RVyYLh7q9TM6CeZ7
50Kmdwcqqld2N6SmTTxWOawEim8fPa2WPze28D2Il4ualrZ03qm7nT+Y8GHU
eVW7iF+9y7tI+PHlG.+vNtJUl8ljOy9Sx2.NVCGZr5Pr6wgerpeiFqN8glWw
f7EXdU8BOVuC.jt6.CKsw+wdFURniGdXwDu7vDMb1z0StYUW3R2MaFO6roqJ
W447GyWve94oKqG6yKK5u6gAoy9ApTS1gK0++cizGmipMoOpBNWJieKqCdqq
MAksSk0trhWZa.8Lbud75I.ZaKi48VeCuqAsiy6QCQmOEqACX8cXrxyld4jC
NtMAIsJ1Opr.6MzbveRF84i791prVOiZ0K7ntupntZ1ha2p.p6wluxVplXz7
3z15zGp7n5T98b4Qi52zxipS+EU4QWOZ1nYG2hgIBGO5f1XLI7mrxkvAed5N
I+YurcfPuUD9poqtc13ucHTDgRJGs5TIg0giON2MEr6NPc+0J+1bkeS05lDS
+0J+9Wq76esxuubU98KS95sKG8+5y5Q+c3mlQ+eVc43YiWRU5Q5ijOYDmaIq
wUG.5XnwRMzWJleGWKlVpOkwWq0at16J4gn.U12urDbcSu4taf5Si7EeguDc
CYyB7dt3u2CopWXUwJrph+nQ4PaRLGrTcuiadBDiFvPr7nUyLTzbr4BnK2PT
+Rcz89UPArkYD2QSLEQGxLHLE+6ZlRKMTRn1E.13GygXz6cvWjSGyCT2kni5
2urn69SSaqmRxpcBUF+ZWUxauAS596CYLVGeJlie85PoYSZqG2zNasN4ChDj
8ctKpQmb2IYhwSqm1NbeIoCu08kzqdyknSl+xq4RL1REWB0v.NdCknS1+hog
RJxvMUf7hW2WrBj2Z4weYohBbq1nizKYabTmULu8zAU2aieD7u37i1jOdI4G
s1bMujsRh9DngWr12nQZ3EU1r0F64kjFHvw1zSi5Wb5P+NfNrMqm9xNuzt8B
2KJcnOI+Z+EcaN0WofSGnNVdWon9tf+wEMsVaK9y8V0pvluWwcJfxlbl+RUb
39FlpCVtN6SdXFeeML2jr482zZkoSaPsmwY7viyz6royFFmNu8zGm42lw4mu
a9kESEGunx6SJ0ntOP6i84Ee98AX+fu8+qmu.utYSu7m1dvsSVId5KI.zt85
e.OaD7TMYEa3oWs3lwSKVISaym2hk5jiN9pqtcwz4qkvuz01sv3xNuKkBAiJ
ES3PmWd57TAqx3zVULn0wP4TV4TwnM3R9PJYcp5obcmRE7ln1FMVsIVNkudJ
swF0JKzg36rblfzzGYky6MrUvTImci6jSTR.NSVeP4.oajrXXjCQPIYqMhwA
aohZMRbGRHn206A8lRy+baBuArqzVNdNjNFsIaXGfgrulaLDZq2F2O+3MpS7
tbwrYils3tqnlx+vcK+B.WbzQ+daDQsNzXK1b9gZ0lf9D5.kNUUNJ9zUiWO9
g.i1r5bDcafDIW1iSnxOM4a6l8ly9x3Y2MYSKWoUdS1pc1jWkqc8DzPSpDTD
yPiTNTf1ExQW1qJFAvgRQm0D7Yn7GkqxGbFCPAnBkbcyCAsKWJ3cdMbpTOjx
nz5jSmBlTbChw8gWUHdceDuIDbJmxa8vvks7zi1rIAaYf7CER.RyYm0yzumS
o5gvjKz4UNsIfY+xghNWH5sVcFBAwxg7wfyaTlHtYlfMZ6RgwM3NjqoBsP6l
9n8nUAiOIvjoMuBsCtdxBalAOXq45grXb.hylwjjWtpXz3MdcJ6TEhW4BF7u
vwv04pyEFmOZvQS.CuOVOjRkBXjji4lHcaejNsbq0YX3OhY+5jpNA1oGzHDG
pzYUlR6yFmxX6jYR3eE8bnKWEbFnf6XSNoMxg73YCrGoP128nzNmCxjIiwZa
g1c8Q6V3pJYiI5CRj2cbr.thG9er0CAla.h6P7FdrqyDNLA.7BfLffbc33ne
wTJacH7m5TnEvITFL8jLYW8FMZWVmsIZSM1Di22qxJTMAqADQBbh5S2FwDO3
fIamBFDqUj6Q1bpprBkPv4Afmrti3gGuTNjvUlwyUtJbDvdfliRDiBTG06wc
B+7MorF5k3AHCf3BFCyf9jI+Xf1OrICNgvsTIXswYrFf4ndHXPwDApAHk6jq
BR5k+oEyFxgTVLApxZXgJ55rZksf23wrsM2BwG6UjO.QVP1zDX0hAsAjALEv
ZfATwlHrFAxhFLDtrN.UhLLAEsZQPBh2V97rzVoXv06vYcUQvyqpXPwGxZYG
LAkZgzS8R5PjA1D0vLi2WsJCm7tXNlbQkJ1MZvbiKjUb5PncKOnAVHyYSry0
.DkgNH7UnBc2HD9ogeusi3gjG3LAHHB6AsP749EZvLLTcfMWuvRMZvYfjcly
HUZvfgBjGhYXqTnAHLDfbiJmywfUzMIS.GFSN5JivjMAXBVawUJOJC88kggR
v2ZxTiV0OmGVfAzRX3.nfENuxGg+vHDCjICMut.Ac4UhrrF7SpCB4oPryQJL
RBYB3rsyDONjGtpyAeRaENeBl2osrLkCah5624JbwDocWH7JS+tnG5bQqI4D
cSewHM0KfCUa2gfZ.lhf0ZQuH.6OPV.5E.OP8pvvKh4OZmRoqJFAiWwuNZ99
bsQ785cElsvrerXJqJj.XGDYKjow+up3A6jv.OD4geoPt5z2PU.LKA6+1pOX
HfCpGiZHxA7fUevH1FSBBc3oKl4wilSMdDkY11FrldcvVrY.oPFfk30GhGVZ
O.1ZjWH35fSooMBXZtdHHXAIohEaw4FjoTkvovHT7uhyCvGYZ1WIZKzDKlYr
zrax2Dw2qGVn.YnmZPdFwuOdiIfXHZ.lAADClF.fKXhv6ko+LvtDBHZwrQ2g
9AWAbgwH0qZAQ9sxPu2P.QzBviwmbFn7Cqw5lH897uhWqEBIfcQnSENCL2AK
OPO.xxv+U4Pf.gAUfJKAemE4AGd2.PQf8AC.8TNDh+EVzQ.Ev8bcP63PDdug
tMB4rKBZ3SzZAqJDai362+pmuKE8jFEjGvaBP.5YzsZQZH.aHFD1qoyMlGZk
vyFDzHbZQLBnG0PMGtuzhleFda8HB23FLRlHiQBNMfzWnIq75dcuhWWFDEbH
AluXM.1jyjQIFlgX.Di8v9tExWUES.DGvmiYHYUCAAdQANXDYBdbNQiVQf8L
qCfv6vYSXfvmFv26aBWftWuqZ5DEVFf1pUfzZIQ.fSQNXDWOdvdSfUCC3BSF
9TCVvpgTQnJXAAHHZSDjfoVCmAXLvPwRf6QIVLLMkfbJPEfoCeaFZ508JS7C
roE4zuOKjJXNFZhP2M2CicIbXvkkXpTz+NTSQbivLeP.CCdokPj5FO3gB0Wf
YEDJBppJzfPFBftYJFLMYnwzenqvFu1Q4c3MpCqMSnGFJ3EJTOPr.y4zyElP
jC4AJNHp3g1tbDP23R.jXWmpBPLRv9.+.FhBNMFFriHFbg1Lwa506JLvCieP
2GPPrUAUfV.gnB4VBrobDvhAVqb.PoPjhEKFH7IH1fvagS+bQdiXrfuHDKYw
rU4FYXi.sMLVB1bU3BQABaV3+AQUSSdWM84cEdDIrCXpFFW7Zg3CzFABbEFr
quQO0kg2TJiWUMvDObv.EVfYIZEevEchH7ACwlJeNCisvSWxQvEaPPXo0VBi
11jwFSedWAjbXB2g.z.T2p+bHglghLzQAWp9FsLeA.4ISObpZuw5YTWN3P.W
SMBFvlQXqvrKHe3Bn9rfsUH8.eAlPcZLQEUlw.X4U2VVC506Jl9LvIJvJgAQ
k2vfvALSelBKUFX.ZdLHDDPdE+.lx.dyXhAzokTkjXzqZ5bF3HD+qvVfSoXB
R5BL.h5IBWE1Ygu1lH9dieM.i5LGQIpG4k2HvC6fodZPP2cHZEmHjAF7tC44
plihwnrAxBb3mIXfTr9rTL+craTCXtUhzAdt3MgW.hPtIpuWGrPmGtWgzCXN
BprLv0iQC9IFEhSIXDDJF9PBQEInLgEIlacljYwmDMxBD8pLAnIyFDCCcbA0
dAIM.S57PfClQazdS+dXM7St0Pi5cAyQ32dlgHDxemHALAwzOAf6QwMOz47P
Dvxgs.Yf1Y.+DBIPMPfySrpdDSF0REvnk7HhwNisoIurl97xBKMvINy6DPyV
sVBTlQl4LPCvrPU+zQXDLGdVJXWQgAamPgMPiel5Q.GFVfTznTMVDnmCQDnI
nYh1hBvLCSKGrRiC0lTeeNYMLJa5v.V200zhBSaNmMCtHrEWw6.G5.uHP9BG
U4JwawrQf4a.QrB6ekCAQPbIr7UvOP01ECC.5uFFhPclEHFfAI5UmkXoIur1
d8xRYDXlrXZTLu.nTH5HEA83DTCv0Y.TkFHxLRb5XDS37ALJcRPe.f.Lp6XX
fVA0umdwcvNuhPsqOdvRXVjMXHzlfis+fX0vTnpDFcJHALXn4.nNxf05xsGr
EloCTfePR7EbymcTzv2kEReQnAZ6v6T2gnAV.8Ci8tPCAuBRj7gSwwlndS+7
dP8YhlEzq7Fo2HBuABlx.hIkJvL4AG.BiFikHGUQl5FQOFxDPyMRgpbmImDi
ROvXwjCQ2FPLB2E700FuuW+rkXEbDlEX9UAS9kB.rIvPBLXJxpfUCdHjuHj+
pxGlIHn.MD8qndfpMhcTiK1H93.3SXgkIVElaqNNLv9OLE.kJXcpsb2X6OJ1
.Quq8TSRB9DTDCsnfU11I1GgAFHp.GTc45vSIsD0tMYQS.bWVzSniDbB.ZXK
FtIBLyHIeWR7yLmEDfmusDz2uiVvsRF.CD74JJgGWh28TZ28TR28TJ2GWB2G
V51lH9PunK8LuiLO8TnthtLCK1vIDvwGjx5DI7FO8rhoJQTx3XZZ.VNls1Jf
SSYrPzkhIT9fwch.sblM4BO4SLG9LRNUa1Ki8R8.eUTQSDIkSLsin+fvIlcA
XDaMU.L86DNQTEqwtTfn.TzAFicUm0UxcXIeCDejLAAT8XPBij5p3EzRbv4L
SQNX8sQ88FNKDYgfKPnAnwYA.nEyCLmq9XGxQOcEv.irvxtXuDz.DiTEeQUY
BLI.QlHyEHtdwZObDiYNHgqSh4X7FwTArgAOMMAxw1a3rHttBHWaDNmpnPxQ
5nBwAgfKpAiCgoDSEHz2fBWEgdIUkDXJqPVMtDJIArDP9AFeDwdBFiH9YAcD
foLbPV6KljmlvI350SKiMRwROSWGgtGObHA6FlMUTH6cvGKf0iHQknpXEerE
XFPfQ.lBGPJBsiZsBoFYUUXjVFopPNFl.A7Cg+1Dbb8GOKcKlYM07RtsfzLU
ig4QaczP2svfIwHPFKOD.4Su+QLUXqxCzoEfCvhWAxudHB5CNj.dB3MoZ5BA
wADpPTC3FZKOBNS+jNjICjTiAUmyRHNCmRHL2XMNHshIpmnOYU+jpAmYHJfN
XV1pAYCmlYBU0wD6UcxlMzjPQyR7gCoyDqUgi08oofYc8lpXhQBAZ.LsLz9Z
ZJfKEn75oWTorCH.WX8LxzMYjPW37SsJPrZtRHUTMFVZY1NkDpXIfGZWO1EU
BznYNIngqfpIEVmq+rmA6kLGEbsPRHBFGNSaO7tHlafHDvCXJ3yDQW5KvpgL
hu1+VkJ6VRMLiC2JLZ.x.3AJVV0cEjiUMAus.igqI3Ytd8xpXvGQJVCa3RHn
fZ.1C3lBFN5ZmBGoM.yJIAiqzNHSnXhercvFzzPukQBiqJ2UfQX9LvqyH0NT
wpSjA6wy+tIpOzeU7A5Rl.CD11lDbwxIPLvHJDohe.Qhp5VM1UpvDq2FKvBB
+UtnXAdIChpq8Pv7UwU.IYc2SGA7lSEy8sUE+9qGKH.CEA.bqt5nE0AlXgDK
HkH8h4BO60i.QSHx3DaKLW6fmTojeTqHBryTeQDbTIKSVFdCQSWM4vrG8eCC
psUcJW+IMlgAArIJ1nLapJL7nC4R3upqeMPfcv+JvPCySRxYgOePlfUlE6kL
I+r1GYFmkoKIqHfd.Ev.GxaFPHDqDc1ZaLuqtd8xFXg.RrJ2bprZQyyzcGX0
h6pfMhMD9fXlBbcoVNyTvlCkDxJjJ44IKqVDhRudHOCDLR.09t5pCzMAOyBJ
KdZSRN9+rtgm785lE9AsLXbVB+tZ5PGgLsZ.1tT5DZviVTfZYWjdUC1vvXW.
tLcMIH2XzwNKnv7OBQfkGDQaJf+fkp.KqLycTSjdutYY2MoIFXij3ZXqApcH
7P1aIUmKTkCVdPjIQoP95J1yLwwzUmDGBijIbNxtaRh+vvFVrjE1t1cBWEio
D7IHzzDo2mSVZFojSI3Bs5PEXNRrx03cRHg0rOUJy.bnh.rq99sTFHfPrTrb
C0DKQNLqdBmHjLfao6AKyTIaVJQ4gk+BJPPcJ1FeuWerDBHadBD3emWJP0FF
9FfRFMccUFydjmUYKJ.+Y30JBYmIBKzkeXCimmsMRrq.yd1uBLfcuDbqkoxk
EmIRWXMQ885iks8EKL.jSjHmS.XCTXiL8oxvgHtfs+To7MR8BzDbOWqACck8
FleBbrvjbH1UTLq44bA2PWSufgOMdB1VihM8mvXl.QMvyifOECkv1A7q.sKL
JDiaL+0vaVTQ9eWzz3dJcsXrq7ZTtIWJbrRJ5bIUqAntB3GVSWcrfF.jhnAz
1JFtuWWrv+MyAVh8Pg.8yBfrZF9Ay.k3QJB0WVQEKr1KS+YB8m0mjl167a4g
9iifBjLFSAP.tAScttlcjtEc7kZXvmMQ885hESfNZY1WhdPxLGqGNfiPTt0i
vTSQG8AaW+HBjNdBvOvjYK7Ybd3oC.WXljE9LQ.CIIH1o6vGfIW1s.vsUSNX
84CHyy5ZpIdWcmoYXZwAFCgrIYUJ.1EafNnwJ43isWG0Byr9ph2T3zjI0mUv
21AcFWigY+SK0Z2.XGL5dDZrps1PHzq+Ul2vngE0FS30nqgyVtJg.CdDtY0l
GBxk8WPjMaSM5ZGSiIBejcc1l1yoTaSnzFEmc34fHdRvjFLEKcsntjVMVfWf
WpIhuW2qvnlwUyYcV5oFXAwvJkvHkjr9B66dpImXtFCcvJskbVyq0zA4B3BJ
hHa.ZvxBxB4CVijQDLu.b3fSQuasw5M8CqzRBQyNAsCaKdi.DSrDaQGwWZ.p
RA8DcXlZS.Cf4VqKJLJTAeRvBlUP1vYqL7kxx9D5BN.Awx1KjVkZh16MNVZV
DJrrOxBRw7KvKMfLKhNhadESd.vumR9t5SwLOoJsAmPVrBC3IgXriR88AdAZ
vgoFRvHQoJVyJD+FdhMQ68mqXV5nDsrDklMCuFEydclcbqTVC1v1rMVYfTcs
YLgfA2vIDtn3zElIgzEhNk0VTZiBLwvJ5BCwQ4PLssNVeDlbnlBFIzqGVl9p
HahFkzMDZlMFZsg4KtJhvldGPHhDFnRPuk0D5KzeMzhSMmrlDyjJ6iZmS5oE
lcJHLAa.ZQwfwk.TM3cZSsUemPn+FGJUj3oGbwsHcwBiHrUI6ZFTBRyyt9vy
RaWsIA.V4D6B.5gndnRn2XZzn55OT.XJCxD3aXRbjBCoXEFMFDXfoME1dcwl
Y7PXxkoVU9NDbr7Tk9IGFD6vDifgJATCDAcL5HatY1H0NYRix7kB9oXMqDUC
fnPw7LAOsB0CsJ9+YJ+ZK8Gg9ihkQNywPhk4SrQvNgfs6zlvSv7.yJPhIuqK
OSEMaLCvDNInAXZgYUSbRIefwF3w0qPrVtz8cNsicFK6Qu17wF5uwhAOoz.2
FSRxTmFRCb0oFZeYaWXffb.hShNSJ9ogIyiE9gx0cYdfMagslz7M2XIHc5ns
KBeCqXESMG8QzT2n2mSVsm3nxkOz.aTpGFndVMb1EAR8crkruR+MDJYsJPIF
0DE6gZinGGJQJB4NeWtu4GWB8Yyp4HoYnzRKvSEKxbakTN1eQYogDc4StKn6
BYvw9qE9ePXacHKKItGGJ2URYKy4jpzWucsjLKEKhZhCBWraFJnY+tx5XroG
qyLdPLL4XqIp2bfDHPiMvD.De5xmWoQafJK+LLDA.N0vCBY8tu1AlVMNAE6Z
bcVDSGMTASIBRBl64RZQ.iVbYyXrXe7lXYsZi56unrrWdXkGcQAgigKpzrMM
H.mp+ELCyVqfIoDNxpxWDtFwAwFdpFLCyoDrmvPs5jufHOaiNhyiUDQLXh.B
Jdwy6ls6m35BvjatntL2tYYk81kStbyZmbX32HS99RaFCYtC7UDV2t2.vzOx
NAFdRKtmKY9JkZ3aHb+e2fp2lOfxFWUxkkmaLm+b14B7p2l0g7GrRGt2wos7
4e5326um8MHKbEaFI89VmCOkA88xRutaWC2u1Edf4UDAziVVGcMrImbn0rvc
G89SXzaGzo76WKBOjf89Vh.d7xR3IMgaealvqK0fx+63h5X19iveEac2R2q6
4bOluXmTt4+J4V3D9lnO32Fs1bBp+ggiw7+dzAWpOD9QBBDkLpjYVprwLaq.
.U53F75eqnGfQdaLq+8iN3p9gqtpe.A9G6CCQ8cbo+CMjSuMC4+1COKGr0gr
kcaI+X2HT4LBLQWVureVSxuQ9t4Fxy8atK6cAMtXJOjfQd9kGFrrYH8ktiwY
eN13T12t8fnCOjqSyuDC4vayP9Hx0cpx6StV2Bxk9Eryucx0G12sOF5cR9Y4
69j1PwdMEqkY4gWrN6daFw2umX72x8DiFF5V.Ti8BQxmR7Ctfs+lVqdhAbkS
uKcLKXQ1qiYc5Y4XN4eW5WFBxkQ7v6WNYem5VVVcxFdk4X9cp4KYR9EXD+9z
obmZ7dcJaSOGo5n8MLQQGIxRtiA56KxRtTq8Lhrbu7hSIfR2qH.Ete88h.PI
pempgKR7CuFdH8dGfR2PeXAnDdp54kG1tK79U1vCWRfElwiWxrspsWJf6cYT
eqkm4Gwxa9cYBM7tLlc1K3O6Gld0UxN12y5suYLbj29tz3hkWU2sHUOuWNyM
TCrY01qW12+x0uFu7Tu7c4H2Lc2EYTWcuy1jdbpzh15lWwAOoKT2Qp70+Jr8
ZO6.w2K6b7uVh2J8q3650SssraLukTYehO6r1l+PgEBJj.g7wOx5rvuROq0Y
CFhVvV2vae74d1TtuEtT1LHboljzxCyLRSRZI+P7tZxrYkhFdKWO3w12KWMD
CzTSBK9g6ccbUJ2fLA95YBrrTI2v6ZPT3RM8thCx7kuIysN6f8tNlrQzbPqs
5x93mGNZcOrfuoRZhe7odtjsK1BKROHS8tc1Gh5c5HNXuK8qz6x1jX1PXWuH
.YOxqZP7Lt6l.Sexy5g5McL1Gi0paWP548lNl.XLODxD5VdULC2Czqx1xqRO
HuJ2wjzUgAaX4O56xNXuqlDAGlW0Q0qFBNXaHiTCh3tJ0765YKD1VPTpgPfO
29q54yBaxKhRMHrvPyuqm63J2hjQdHfL2Tnb4gf+kcs9ld15vsHTj7Cguwle
SOa+8sH7kFBiswbquomK2KzhTdbPFS5VeSO6wTKRDgGa6qlc6w2d6WlrrqOv
KujytY7OtX4lkGeD9y75+rjpxyVN4Ka5a7x2G0YiWd4OLc8jKWe2x5VH2WkM
0mytYwUSVN+toRxJJcs9YqV+sYOLi5a1849E2c0zE+t0iWe2pO8amL+tZp6w
n5yiua15cYEWb8mmNa1kKlUIus628tZBbV8rmuYWfQt1xWnNWFeqKBhbg5JH
qUfF9AKd+1pX8dzc2DWMiTxhhnQV3f3m.i7A59fayb+6heZa00H0tEsAKODK
i412134WW24iLwMa+WrY8Wb6hkcyob0Wby0e25EWub7USksVX0Ncx+4hjzRb
1Baeqc3uytALzoc2y1RdalL9M2c43CMAL9xKwCdGlp03kEvqxJHScs+tdrsF
m6NQvOxDYUrKaSxBzqGd+dvMMY1jad36Kl3mgKuijhKa2key4KKFXaeuqvMW
1qy18t4migr81DkOQ3jRwBpt8MyRYUtuOMcN0VteQNvlMcqFtcxE08Ugce.s
HotYVrGg0FEf1UbMsQHMEU95BtT5wD3CEWCcycA9ew5uUeRuHRqas620I7AC
W+a2NY9ne234qF86lbyzKVL6py1hitC6gej50u.V9cbWWZ6RbARqL16VY.e1
JD+1wqWeHEBN.973Nyy2G9v1aqe+wxF62.QP+6+h0epbapSTOssY3ckA4xzT
cy1vy0aOYIYOU9V814llMAtDt+NkMLuLWlgquSHLxu6rlzwpaycxO19Nd.S0
7mw5aMeaurJb+hkSGO6.5XZY+O3w+ldvjn+C+9+oSTTlK1PxBiDW6upeRcFs
4Ptbzzie01PpaOsJ146+HtbbbIar53OaB0koOeVWVfPOf741EfcC1tck4JKm
Y0OlTsrtDwkDy5WSZ9sW5tMm6u4Xe1uv8+72tZ4hqmL+2WXQ8HiykHQYgqjK
rFxGNtSkGRQ7RGyL8xSTL2IVZ22u0OzpFuomq027QEt68A8DQweuIWq7oay8
dnp6IdHucXDJ2YPj1f26w+1SRT9fRr+5Iym7kw8JqdrA9PJq9K2Z+gc+RrO1
eeZCKVI+1fSV+J5u58FQ8qGOc9+ciTE6p0N+OO92FdRa0OOEJmmjkGsnvd+O
dQnIy6Jh5eY0rorIKNAYqGPMGB.QiFk2eLqsd2OvZwis+Nj7qeyjqNM8v84I
Xe7pvKJYi34VN8qWtd4rmA0OnDD2+qOnwimi.0CDIdUM87ut3ptcT5FrJ1ni
1mE2XOHXFzA7IYB4kVA8e8tat3vDy9r17Xmlu.j1+9zKWebd0SZldPIykSVM
Y86NzF+tKWb6j1gabeVq4dOprt6bPqDupL4e+3KZenznd99jbNp8kAcPgfqt
3n.n2SHe85o7UDIzuew0LTlACN6AlT3dUPT1EmbxB4mSJqxPNj9+dyQJrzqH
68OL9KS97hk27eO3b3SG8n5i9AZvc03k+z2Oe50+v5uujMfSTtu0DMuIqEmX
dT6IEEtMlBhaJlylx5jJu+AHGb5iHtO3IsXvy+1PVhwerLULYoRIeOdCwi5f
wR9vpSbvzZpN.dQ+QDmtuDKO5WFtre0Fs+9VPpmhQbwrIvkYs.f+xEK9oyFH
iS+3sSm+SmZ4xvnT1LLJiZtjf5NPdWa352aztM7Zdj3680xnb41s+si6PngW
4iLy1v8zmJw467yAHOvsSSuh1eG3JY7vD+dLubChZxOUiI6OvV64sFrzLBk3
3Pn2qJ0FO39M1E6l4OTtQTYmzIJYtwPJ+VLMnQ8by3uF32T8oYLJsabKQQV7
4UOmcF+OXhb3.FxAb4Svt8n7LVuIuqeMJ9qG54gcVHS2Og8T3pOaXhoMMnwi
+sCXqJlRxVc2i+sWQW7Om9TaWsi1lEqeJ+mVR21pm9F77ZTWSD9kytax2qO0
VoSGkZQeuMr71VtFRBb4hed9ISgG015.Rg+Cea7oSfJtR0WMRx8QiptCWIzs
COA9qWNYxSfBKbuMohi6Fal3vSb+VXYa95wmL4U1wrksNEkttKxFC4xlQ0PS
i+GSt5jou3Fja5Mw+nDOFCM88+axrYK94SmEZ70lRJl1r6iAoR+wZlMeVoRu
DC.yeNN.Jku3WuX1SPDYSJj7.wjrjqO3ss1s2s71YOMvCwMcSmS6C0UzdtcX
G8GAgpSUAFY7JYWdyvMEtzPNtVN4xIS+xgqb29jY1DXx8iI018W5vPb0PTnX
Qyd7Cb2fJKNBhRmBCo4r8fb6WGonUSle0p2adPtmIO75d6sMiUQYi+KacxVl
F2q2zCpry5w2drN4dqjQ8aFudwneCiB8rA68uZ8jOe2rYqOsBrvOZk59TUXC
Vcl5iG18oOrwFSdecaQi6Sj0cQOtSxXBCKSsNndgFSCX78lTLUA1X2n5X41M
8fZ8b8jUuu9dA9YlMmucpsAPYWXKVSamUlWfxsTkllx6PieuA6Nv4xA2Qxnn
NmUAY6qz3jZsGTp5lrbdmG7V5y+poKW+sQ+iWu3IoNW+z4JUviOyU2JSgk0G
uu6+569e.gJmv1
-----------end_max5_patcher-----------
Here is the relevant code:
function linearRegression(y,x){
var lr = {};
var n = y.length;
var sum_x = 0;
var sum_y = 0;
var sum_xy = 0;
var sum_xx = 0;
var sum_yy = 0;
for (var i = 0; i < y.length; i++) {
sum_x += x[i];
sum_y += y[i];
sum_xy += (x[i]*y[i]);
sum_xx += (x[i]*x[i]);
sum_yy += (y[i]*y[i]);
}
lr['slope'] = (n * sum_xy - sum_x * sum_y) / (n*sum_xx - sum_x * sum_x);
lr['intercept'] = (sum_y - lr.slope * sum_x)/n;
lr['r2'] = Math.pow((n*sum_xy - sum_x*sum_y)/Math.sqrt((n*sum_xx-sum_x*sum_x)*(n*sum_yy-sum_y*sum_y)),2);
return lr;
}
I also included a vanilla Max version of the mean of the derivative of loudness, to compare the results, along with an option to omit the first frame (which would generally be an uptick).
The included coll dataset has hits from brushes.aif, jongly.aif, and some of my prepared snare stuff, so it’s a cross section of diff types of percussive/drum attacks, and across a fairly wide range of hits, the slope seems to more accurately capture the temporal shape.
When you have symmetrical samples, the results are pretty much the same:
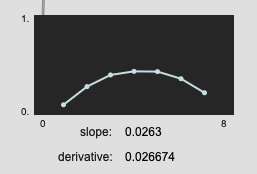
But for things like this, the slope wins out in terms of giving you an idea of what the overall analysis window is doing:
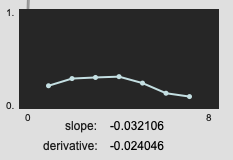
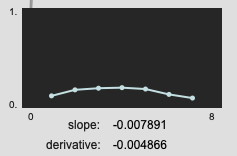
edit:
original screenshots changed since I realized I wasn’t processing the same list of numbers for both.
Although I haven’t implemented it in my code above, there is also the r2 value, which can function in a similar way to the pitch confidence metric, so the higher the r2 value, the tighter the samples fit the slope.
So, I’m thinking of including this as another metric in the timeness descriptor, perhaps also incorporating the r2 as a weighting option for it, so the higher the r2, the more the slope is reflected in the overall timeness value.
I also imagine that you’re in crunch time leading up to the plenary, but wanted to check on your amountOfPipe-ness as to the overall concept here.