I’ve had some pretty decent breakthrough(s) with this over the last couple of weeks after a fantastic zoom chat with @balintlaczko (as well as a few follow up emails), so wanted to bump this thread with some info/examples of stuff.
//////////////////////////////////////////////////
So the main issue (as I understood it) was that neither a classifier nor a regressor (when operating on descriptor distances) created a useful measure of in-between-ness. The classifier-based approaches tended to jump erratically between predicted classes and the regressor-based approaches, while generally interpolating between values ok, didn’t work in this kind of use case to represent the morphing between classes.
Where the big breakthrough came was when @balintlaczko suggested trying to encode the classes as “one-hot” vectors, and operating on that, rather than the descriptors themselves.
So basically taking something like this (a fluid.labelset~):
fluid.labelset~: LabelSet 1574labels:
rows: 156 cols: 1
0 0
1 0
10 0
…
97 1
98 1
99 1
And turning it into something like this: (a fluid.dataset~):
fluid.dataset~: DataSet hotones:
rows: 156 cols: 2
0 1 0
1 1 0
10 1 0
…
97 0 1
98 0 1
99 0 1
We then experimented with a few things, but found the best results by putting that into fluid.knnregressor~ with the incoming descriptors (104d MFCC soup) on one side, and the “one-hot” vector ont he other side.
This meant that when interpolating outputs based on new inputs it would give me something like:
0.951523 0.048477
This could then be operated on and turned back into a single continuous vector, representing the interpolation between the classes.
This gave us a jumping off point.
//////////////////////////////////////////////////
Where this fell a bit short was that although it worked alright (and loads better than things I had tried before), it would still get a bit jumpy in the middle. To mitigate that @balintlaczko suggested manually adding an explicit in-between class. So I set about creating some new training (and performance) datasets that had 2, 3, 5, and 8 classes, which was easy enough to do, as my snare looks like this these days from other experiments:
That led to these initial results:
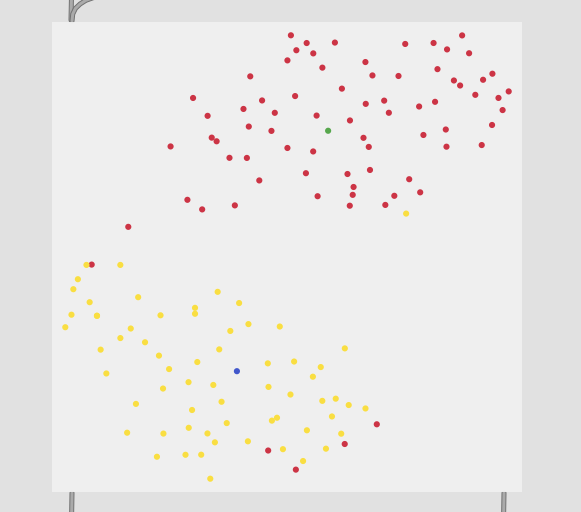
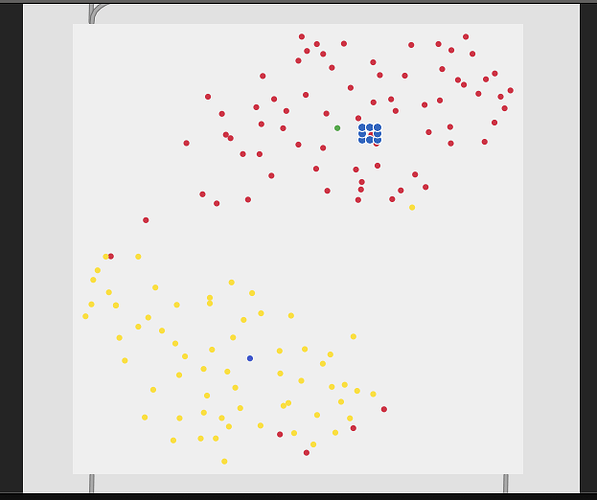
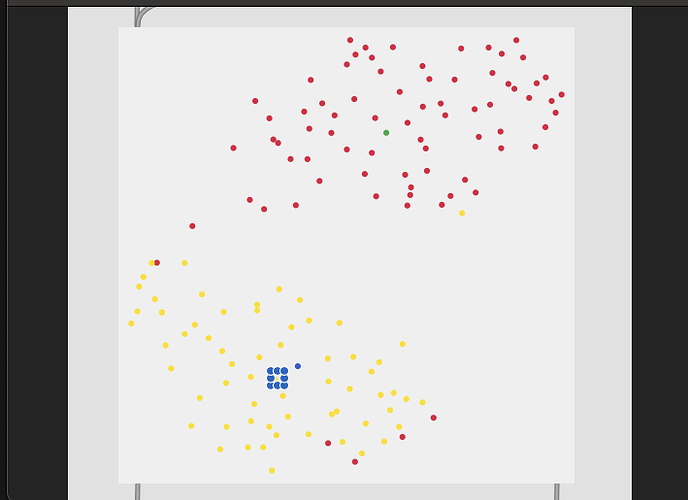
You can kind of see this in the video, but here are the plots of the classes for each.
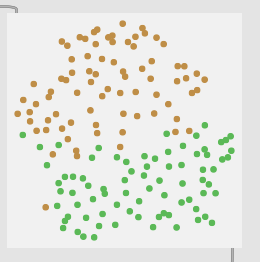
2 classes (center and edge):
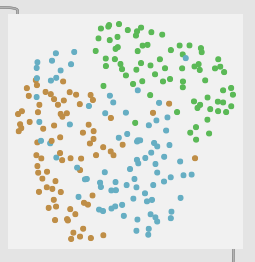
3 classes (center → middle → edge):
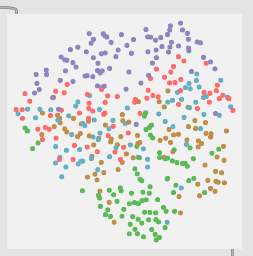
5 classes (middle bits between the middle bits):
8 classes (as granular I could be with my pencil marks):
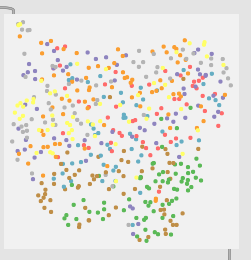
So with these you can see clear separation between the two classes in the first, then varying amount of overlap with the rest.
At this stage I think either the 3 or 5 class versions work the best.
//////////////////////////////////////////////////
I did also experiment with fit-ing fluid.mlpregressor~ in the same way, but this didn’t give good/useful results. Firstly it was really hard to train, taking a long time for anything above 3 classes (and I never got the 8 class version to converge at all) and then when it was properly fit it seemed to actually learn the “one-hot” encodings too well. Meaning that I was back to square zero where rather than interpolating between the classes, it tended to jump between them.
Here’s the vid I made showing that behavior:
//////////////////////////////////////////////////
At this point it seemed like the results were already “usable” (though not perfect) as long as you manually trained interim classes.
I still wanted to smooth out and improve the scaling a bit, so I experimented a lot with @numneighbours. I believe for the initial video I was using something quite small, ~@numneighbours 5 on a dataset where each class was ~80 entries.
I then experimented with going really far in the other direction with something like @numneighbours 80, so almost a 1:1 of neighbors to amount of entries per class and this worked a lot better. Or rather, for this use case, produced more consistent/smooth results.
I then coupled with this with some reduction in the overall range so the first class was more “0.” and the last class was more “1.”. Something like zmap 0.3 0.7 0. 1..
So far this is working pretty well, and although the 3+ class versions are a touch smoother, the 2 class versions are pretty usable as they are.
//////////////////////////////////////////////////
As a sanity check, I wanted to see how this stacked up to the interpolation you get with the native Sensory Percussion software.
I fired up the v1 Sensory Percussion software I still have installed (they did come out with a big v2 update last year) and ran the same exact audio into via TotalMix/Loopback and was surprised with the results:
The results look very similar to what I’m getting with the “one-hot” approach! (i.e. kind of jumpy, not using the whole range, etc…)
Overall it looks slightly better, but it’s not this “perfect” interpolation between the classes that I was expecting it to be.
//////////////////////////////////////////////////
So all of this up to this point has been working on the descriptor recipe that I developed/tweaked over the last few years (outlined here).
Basically this:
13 mfccs / startcoeff 1
zero padding (256 64 512)
min 200 / max 12000
mean std low high (1 deriv)
Previous to the last few weeks, the best results I had gotten was trying some stuff @weefuzzy (and @tedmoore) suggested in this thread from a few years ago. In short taking the 104d raw MFCCs and reducing it down via an automated PCA thing to keep 95% of the variability of the dataset intact.
When I had the initial zoom chat with @balintlaczko I had prepped some of this and while it worked ok, it was pretty shit. But now that we had a different/new approach, it was time to revisit combining them the approaches (“one-hot” + PCA).
I set about to do this only to realize that since I was operating on the labelset directly (to create the “one-hot” vectors), that that part of the patch/approach wasn’t impacted at all. What was impacted was what was fed into fluid.knnregressor~'s input.
While starting this up I found I got awful awful separation between the classes when using this 104d->PCA95->normalization. Check this out:
2 classes of 104d MFCCs:
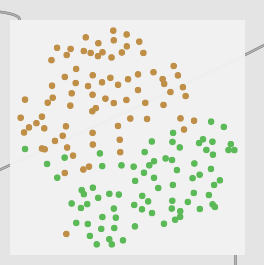
2 classes of 31d normalized PCA:
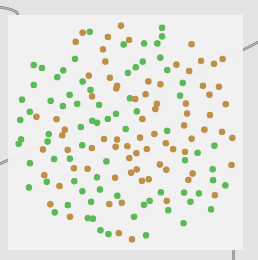
Everything is all blurry and mushed together. Although I didn’t test this data in a vanilla classification context, I would imagine it would work terribly.
After doing a bit more poking/testing, it seems that the normalization made the (reduced) MFCCs pretty erratic.
If I instead use the PCA reduced version but sans normalization, I instead get this:
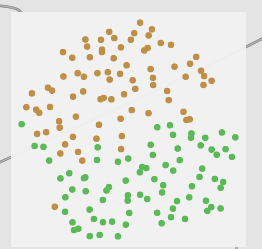
Which looks functionally identical to the 104d MFCCs.
More than that, they perform almost identically:
There’s some tiny variance for some middle points, but overall it doesn’t seem to make a big impact here
//////////////////////////////////////////////////
So that takes us to present day…
I still want to test some more stuff. @balintlaczko has suggested trying some spectral descriptors/stats (rather than MFCCs) which I plan on setting up. Given how well the MFCCs tend to separate the classes in the plots above, I’m curious if this will work better, but you never know until you try.
I also still want to refine the @numneighbours “smoothing”, specifically as a ratio vs the amount-of-entries-per-class. I have a feeling that 50-100% works well for something smooth (and 2 input classes), but given more explicit middle classes, something lower is probably better (20-50%).
I also want to test it across a wider range of material. So far I’ve mainly done the center/edge classes, as these are pretty worst-case-scenario in terms of similarity. Here is a plot for rim shoulder → rim tip for example:

And here is a 6 class version with center/midd/edge + rimshoulder/rimmiddle/rimtip:
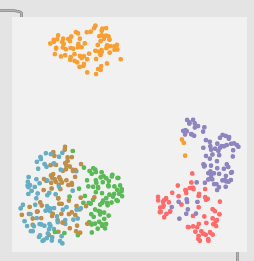
Although I haven’t actually tested the 6 class version, the 3 class version works about the same even though the gaps in the plot are much larger.
Seeing this made me wonder about trying to incorporate a @radius-based approach in addition to (or instead of) the @numneighbours, but sadly that isn’t a possibility with fluid.knnregressor~. Perhaps by packing stuff into a fluid.kdtree~ and requesting all the nearest matches and doing the math on the manually or something. Not sure.
//////////////////////////////////////////////////
So yeah, wanted to bump this post with some info/updates. If anyone has any thoughts/suggestions, that’d be very welcome!